❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
※ prerequisites
앞서 단일 변수 $X$로 $y$를 예측하는 기저함수 기반의 여러가지 모델링 방법을 배웠다(prerequsities 참고). 이러한 방법들은 단순 선형회귀(Simple linear regression)의 비선형으로의 확장으로 여겨질 수 있다. GAMs은 features $X_1, X_2, \cdots, X_p$ 각각을 앞서 공부했던 기저함수를 기반으로 모델링하고 가법적으로(additively) 연결하여 $Y$를 예측하는 모형이다. 결국 다중 선형회귀(Multiple linear regression)의 비선형으로의 확장이 되는것이다. GAMs 역시 선형 모형처럼 양적 반응변수(quantitative responses, i.e. 연속형), 질적 반응변수(qualitative responses, i.e. 범주형) 모두에 적용 된다.
GAMs for Regression Problems
GAMs은 다중 선형회귀의 확장이라고 여겨질 수 있다고 했으므로, 일반적인 p개의 features를 가지는 다중선형 회귀 모형식을 먼저 써보자.
$y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip} + \epsilon_i$
위 모형에 대해 각 feature와 반응변수(response)간에 비선형적 관계(non-linear relationships)를 허용해주기 위해서는 $\beta_jx_{ij}$를 비선형 함수 $f_j(x_{ij})$로 대치하면 되며, 이러한 모형을 GAMs이라 한다.
$y_i = \beta_0 + \sum_{j = 1}^p f_j({x_{ij}}) + \epsilon_i = \beta_0 + f_1({x_{1i}}) + f_2({x_{2i}}) + \cdots + f_p({x_{pi}}) + \epsilon_i$
위 식이 GAM의 한 가지 예이며, 각 $X_i$에 대해 $f_i$를 씌우고 이들을 더하여 $y_i$를 예측하기때문에 가법 모형(additive model)이라 불린다. GAMs 게시판의 이 글에 앞서 배웠던 단일 변수에 함수를 적합하는 다양한 방법들이 $f_j$가 될 수 있다. GAMs의 최대의 장점은 반응변수의 예측에 이러한 방법들을 이용하여 가법 모형을 적합할 수 있다는 것이다. 시계열 자료 예측에 사용하는 Facebook의 prophet도 이러한 GAMs의 아이디어를 이용한 대표적 모형 중 하나라고 할 수 있다.
다음의 그림은 year(급여 정보가 기록된 연도), age(나이), education(교육수준)을 이용하여 Wage(급여)를 예측하는 데에 GAMs 모형을 적합한 결과이다. year와 age에는 natural splines를 이용하였으며, education은 범주형 변수로 계단 함수(step functions)를 이용했다. education의 경우 5가지 수준으로 구성되어 있으며 dummy 변수를 이용하여 코딩했다.
$Wage = \beta_0 + f_1(year) + f_2(age) + f_3(education) + \epsilon$

natural splines(year와 age 각각 자유도 4와 5)와 step functions은 결국 일반적인 선형 회귀모형의 꼴과 동일하기 때문에 위 모형의 적합(회귀계수 추정)에도 최소제곱추정(LSE: Least sqaures estimation)을 사용할 수 있다(prerequisites - 다항 회귀와 계단함수, Regression splines 참고). 즉, 위 모형은 spline 기저 변수(basis variables)와 더미 변수(dummy variables)들로 인해 거대한 design matrix를 갖는 linear regression을 수행하는 경우라고 할 수 있다.
다음의 그림은 year와 age의 모델링에 smoothing splines를 사용한 경우(각각 자유도 4, 5)에 해당한다.

$X$ 각각을 smoothing spline으로 모델링하여 GAMs을 적합하는 것은 natural spline을 이용하는 것처럼 간단하지 않다. 그 이유는, smoothing splines의 경우 최소제곱추정을 사용할 수 없기 때문이다. 그래서, R의 $gam()$ 함수와 같은 소프트웨어에서는 smoothing splines을 이용한 GAMs의 적합에 backfitting algorithm을 사용한다. backfitting algorithm은 여러 예측변수를 포함하는 모형에 사용되며, 다른 변수들은 고정한채로 기저 함수를 기반으로 모델링된 각 변수를 반복적으로 갱신하는 방식으로 수행된다.

backfitting의 장점은 하나의 함수를 업데이트 할 때마다, 해당 변수에 대해 적합된 함수를 partial residual에 적용할 수 있다는 것이다. 예를 들어, $X_3$에 대한 parital residual을 $r_i = y_i - f_1({x_{i1}}) - f_2({x_{i2}})$이라 하자. 이때 우리가 $f_1$과 $f_2$를 알고있으면, $X_3$의 비선형 회귀에 대한 반응변수로 partial residual을 사용하여 $f_3$를 적합할 수 있다. Figure 1과 Figure 2는 꽤 비슷해보이는데, 사실 대부분의 상황에서 smoothing splines 또는 natural splines를 사용하여 GAMs을 적합한 경우 둘 간의 차이는 작다. 물론, GAMs의 적합에 꼭 spline을 사용해야만 하는 것은 아니다. 당연히 국소 회귀(local regression), 다항 회귀(polynomial regression), 또는 앞서 살펴봤던 기저함수 기반의 모델링 중 어떤 것도 조합하여 GAMs을 적합할 수 있다.
GAMs for Classification Problems
$Y$가 질적변수일 때도 GAMs을 사용할 수도 있다. 간단하게, $Y$를 0또는 1 값만을 갖는 이진형 변수로 가정하고 로지스틱 회귀모형에 대해 GAMs을 적용하는 경우를 설명한다. 이진 변수에 대한 로지스틱 회귀모형은 $x$에 관한 선형 함수를 통해 관측치가 class = 1에 속할 사후 확률(posterior probabilities)를 모델링한다.
$\pi = Pr(Y = 1 | X_1 = x, \cdots, X_p = x_p) = \frac{e^{\beta_0 + \beta_1x_1 + \cdots + \beta_px_p}}{1 + e^{\beta_0 + \beta_1x_1 + \cdots + \beta_px_p}}$: 로지스틱 회귀모형
$log(\frac{\pi}{1-\pi}) = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p$: 로그 오즈(Log-odds) 또는 로짓(Logit)
우리는 로짓에 $X$와 $Y$간의 비선형적 관계를 허용해주기 위해 GAMs을 이용할 수 있다.
$log(\frac{\pi}{1-\pi}) = \beta_0 + f_1(X_1) + f_2(X_2) + \cdots + f_p(X_p)$
다음은 앞선 회귀 문제에서 이용한 Wage 데이터를 연 25만달러 이상의 수입을 벌어들이는 경우를 $Y=1$로 코딩하여 GAMs 모형을 적합한 결과이다.
$log(\frac{\pi}{1-\pi}) = \beta_0 + \beta_1year + f_2(age) + f_3(education),$ where $p(X) = Pr(wage >250 | year, age, education)$
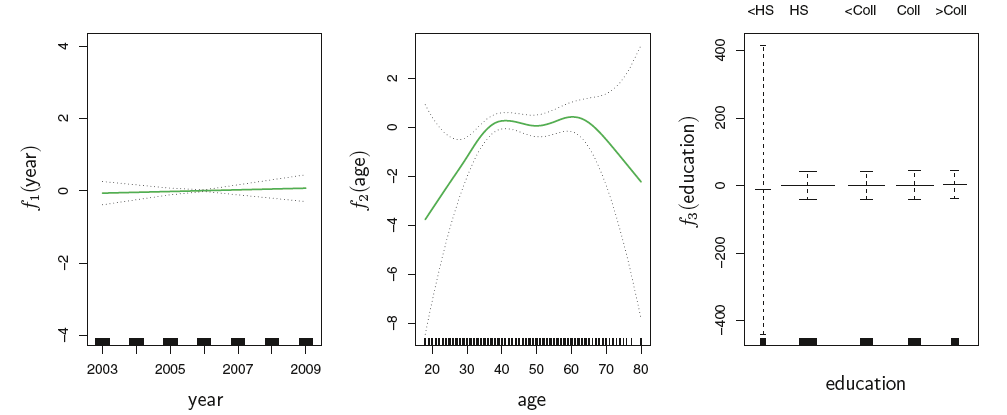
year에는 선형 회귀, age에는 smoothing splines(df = 5), education은 각 수준을 더미화 하여 step function을 적합했다. education의 경우 고졸 이하 수준에서(<HS) 신뢰구간이 매우 넓게 추정되고 있는데, 이는 해당 범주에 연 25만달러 이상을 벌어들이는 사람이 없기 때문이다. 이러한 이유로, 연 25만달러 이상의 수입을 벌어들일 확률을 이처럼 로지스틱 회귀모형으로 모델링하는 경우 고졸 이하인 사람은 제외할 필요가 있다. 다음이 이를 반영한 그림이다.
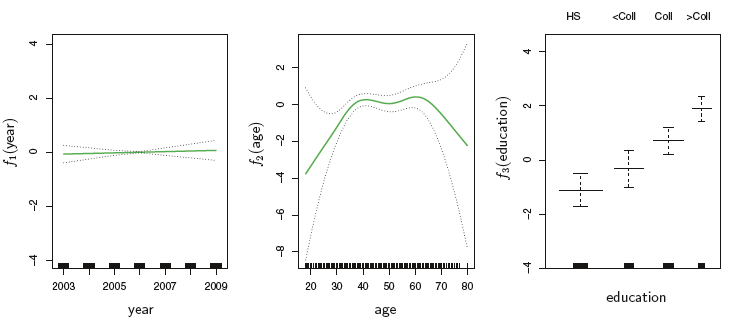
Figure 1, 2, 4 각각에서 그려지는 3개의 패널 모두 $y$축을 같은 단위로 그린것으로, 이를 통해 $Y$에 관한 각 변수의 상대적인 기여도를 평가할 수 있다. Wage 데이터에서는 year보다 age와 education이 훨씬 더 큰 기여도를 갖고 있음을 알 수 있다.
GAMs의 장단점
GAMs의 이점과 한계에 대해 요약하고 글을 마친다.
GAMs은 일반적인 선형 회귀모형이 놓칠수도 있는 비선형적 관계를 반영할 수 있도록 각 $X_j$에 비선형 함수 $f_j$를 적합한다.
비선형 적합은 잠재적으로 더 정확한 예측력을 보여준다. 다만, 모형의 해석력은 떨어뜨린다. 그러므로, GLM과 GAM 둘 간의 예측성능에 큰 차이가 없다면 더 간단한 형태인 GLM이 선호될 수 있다.
모형이 가법적이기 때문에, 나머지 변수들을 고정한다면 여전히 $Y$에 미치는 각 변수 $X_j$의 효과를 알아볼 수 있다. 이러한 이유로 만약 우리가 변수 효과에 대한 추정에 관심이 있다면, GAMs은 매력적인 선택지 중 하나가 된다.
변수 $X_j$에 관한 함수 $f_j$의 smoothness는 자유도(degrees of freedom)로 요약된다. 에를 들어, 자유도가 작을수록 smooth한 곡선을 적합했음을 의미하며, 반대로 자유도가 클수록 knots을 많이 놓은것을 의미하여 곡선이 더욱더 꾸불꾸불(wigglier)해진다(bias 감소, variance 증가).
GAMs이 갖는 한계점은 아이러니하게도 가법성에 있다. 이는 데이터에 많은 features들이 존재할 때, features간의 중요한 interations(상호작용)을 놓칠수 있음을 의미한다. 그러나, 선형 회귀모형에서 interaction terms을 직접 추가했듯이(manually), GAM에서도 $X_j \times X_k$를 추가적인 예측변수로 포함하여 모형을 적합할 수 있다. 예를 들어, 저차원의 interactions $f_{jk}(X_j, X_k)$를 모형에 고려하면, 해당 항은 국소 회귀 또는 2차원 splines와 같은 2차원 smoothers를 사용하여 적합할 수 있다. 마지막으로 한 가지를 더 언급하자면, 고차원 데이터($n \rightarrow p$ 또는 $n < p$)에 GAMs을 적합하는 경우 OLS 회귀에서 발생하는 회귀계수 추정 문제(해의 uniqueness 보장 X, 회귀계수의 분산이 매우 커짐)가 똑같이 발생하며, 이 문제를 해결하기 위해 OLS 회귀에서 Penalized regression models(i.e. Ridge, Lasso, Elastic net, etc.)을 고려했듯이, Penalized GAMs이라고 할 수 있는 SPAM(Sparse additive models)을 고려할 필요가 있다.
참고 문헌
James, Gareth, et al. An Introduction to Statistical Learning. Springer. 2013
'Machine&Statistical Learning > GAM' 카테고리의 다른 글
| Local regressions (0) | 2020.06.10 |
|---|---|
| Smoothing splines (0) | 2020.06.09 |
| Regression splines (0) | 2020.06.08 |
| 다항 회귀와 계단 함수 (0) | 2020.06.08 |
| 선형모형의 한계 (0) | 2020.06.06 |




댓글