❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
※ prerequisites
기저 함수(Basis functions)를 이용한 두 가지 모델링 방식을 소개한다. 먼저, 다항 회귀와 piecewise constant regression을 결합하여 더 유연한 적합 형태를 보여주는 piecewise polynomial regression을 소개하고, 여기서 더 나아가 제약을 통해 piecewise polynomial regression의 연속성을 개선한 Regression splines를 소개한다.
Piecewise polynomial regression
piecewise polynomial은 $X$의 범위를 나눠 각 bin마다 낮은 차수(low-degree)의 다항 회귀를 적합하는 것을 말한다. 예를 들어, piecewise cubic polynomial은 $X$의 각 bin에 다음의 cubic regression model을 적합하는 것과 같다(cubic regression : 다항 회귀에서 $X$의 차수를 3까지 고려한 것).
$y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \beta_3x_i^3 + \epsilon_i $
당연히 이때 회귀계수 추정량들의 값은 각 지역마다 다를 것이며, 회귀계수가 바뀌는 점을 "knots"이라고 부른다. 즉, knots이 없는 piecewise cubic polynomial은 cubic polynomial과 동일하다. 예를 들어, 단 1개의 knot을 점 $c$에서 가지는 piecewise cubic polynomial은 다음과 같이 쓸 수 있다.
$y_i = \left\{\begin{matrix}
\beta_{01} + \beta_{11}x_i + \beta_{21}x_i^2 + \beta_{31}x_i^3 + \epsilon_i& \textrm{if}\;\; x_i < c; \\
\beta_{02} + \beta_{12}x_i + \beta_{22}x_i^2 + \beta_{32}x_i^3 + \epsilon_i & \textrm{if}\;\; x_i \geq c
\end{matrix}\right.$
여기서도 각 polynomial functions에서 회귀계수 추정은 LSE(Least squares estimation : 최소제곱추정)를 통해 이루어진다. 더 많은 knots을 사용할수록 더 복잡한(flexible) piecewise polynomial이 된다. 일반적으로 $K$개의 knot을 사용하게 되면 $K+1$개의 다른 cubic polynomials을 적합하게 된다. 여기서는 예로 cubic polynomials을 들었지만, 당연히 다른 차수를 고려할 수도 있다.
Regression splines
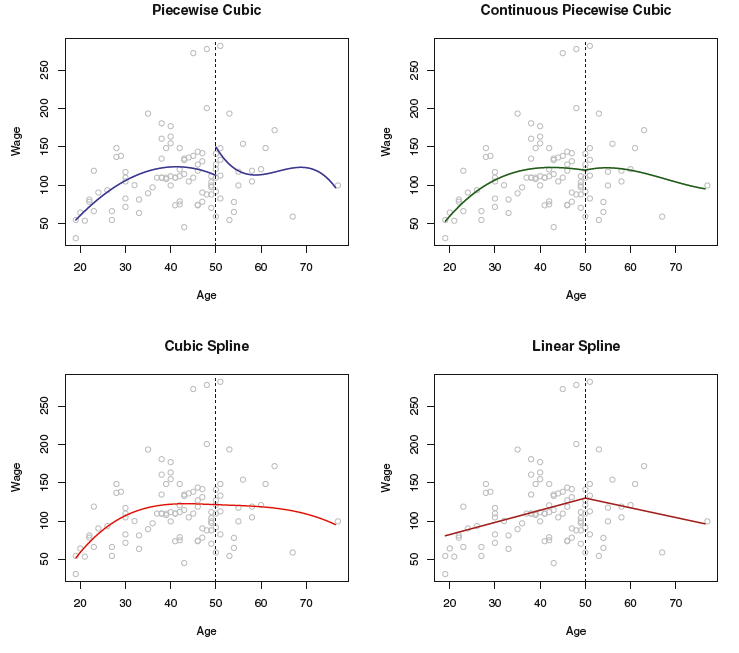
Figure 1의 왼쪽 상단 그림은 Age($X$)에 따른 급여($Y$)에 대해 age = 50을 knot으로 하는 piecewise cubic polynomial을 적합한 것이다. 이때 knot에서 함수가 불연속적으로 이어지는 문제를 확인할 수 있다. 이 문제를 해결하려면 곡선이 반드시 연속적이도록 하는 제약하에 piecewise polynomial을 적합시켜야 한다. Figure 1의 오른쪽 상단 그림이 그 결과이다.
Figure 1의 왼쪽 하단의 곡선에는 2가지 더 추가적인 제약이 존재한다. 두 가지 추가적인 제약의 결과, Continuous piecewise Cubic polynomials과는 달리 knot(age = 50)에서 1차, 2차 미분계수가 모두 연속이된다. 이런식으로 piecewise cubic polynomials에 가해지는 각 제약은 결과적으로 piecewise polynomials의 복잡도(complexity)를 줄임으로써 자유도 1을 가진다. 예를 들어, Continuous piecewise cubic polynomials의 경우 제약이 1개로 총 자유도가 8(모수 4개, 2개의 모형) - 1 = 7이 된다. 왼쪽 하단의 곡선의 총 3가지 제약(연속성, 1차 미분 연속성, 2차 미분 연속성)이 존재하여 총 자유도는 8-3=5가 된다. 이를 Cubic spline이라고 한다. 일반적으로 $K$개의 knots을 갖는 cubic spline의 자유도는 $4+K$가 된다.
Figure 1의 오른쪽 하단의 그림은 Linear spline을 나타낸 것으로, 이 역시 age = 50에서 연속이다. a degree-$d$ spline의 일반적인 정의는 piecewise degree-d polynomial로 각 knot에서 $d-1$의 자유도만큼 추가적으로 미분에 대한 연속성 제약이 생긴다. 그래서, Cubic spline은 각 knot에서 2가지 더 추가적인 제약이 존재하고, Linear spline의 경우 d=1인 polynomial로 다른 추가적인 제약이 존재하지 않는다. 즉, Linear spline의 각 knot에서 연속성에 대한 제약만 존재하여 총 자유도는 4(모수 2개, 2개의 모형) - 1 = 3이 된다.
Basis model을 이용한 spline의 표현
Basis models(3. 기저함수의 식(2))을 이용하면 $K$개의 knots을 가지는 cubic spline의 모형식을 쓸 수 있다.
$y_i = \beta_0 + \beta_1b_1(x_i) + \beta_2b_2(x_i) + \cdots + \beta_{K+3}b_{K+3}(x_i) + \epsilon_i$,
for an appropriate choice of basis functions $b_1, b_2, \cdots, b_{K+3}$ $\cdots$ 식 (1)
즉, Knots의 갯수만큼 추가적인 basis functions이 필요로 된다. 또한, 이 모형의 적합에도 LSE(least squares estimation : 최소제곱추정)를 사용할 수 있다. polynomials를 나타내는 여러가지 방법이 있듯이, 식 (1)에서 다양한 기저 함수(basis functions)의 선택을 사용하여 cubic splines을 나타내는 많은 방식이 존재한다. 식 (1)을 이용하여 cubic spline을 나타내는 가장 직접적인 방법은 cubic polynomial의 기초인 $x, x^2, x^3$부터 시작하는 것이다. 그리고 각 knot마다 truncated power basis function을 추가한다. A truncated power basis function은 다음과 같이 정의된다.
$h(x, \xi) = (x-\xi)^3_+ = \left\{\begin{matrix}
(x-\xi)^3 & \textrm{if} \;\;x > \xi \\
0 & \textrm{otherwise}
\end{matrix}\right.$, where $\xi$ is the knot
다음의 기본적인 cubic polynomial 모형에 $\beta_4h(x, \xi)$를 추가하면 $\xi$에서 3차 미분계수에 대해서만 불연속성을 만들어낼 수 있다.
$y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \beta_3x_i^3 + \epsilon_i$
그럼, 함수는 각 knots에서 연속이며, 1차 미분, 2차 미분에 대해서도 연속이다. 즉, 데이터셋에 $K$개의 knots을 갖는 cubic spline을 적합하기 위해서는 절편(intercept)과 $3+K$개의 예측 변수에 LSE를 수행해야 한다:
$X, X^2, X^3, h(X, \xi_1), h(X^2, \xi_2), \cdots, h(X, \xi_K)$ where $\xi_1, \cdots, \xi_K$ are the knots
즉, cubic splines에서는 결국 $K+4$개의 회귀 계수 추정이 필요하다. 이러한 이유에서, $K$개의 knots을 갖는 cubic spline의 자유도는 $K+4$가 된다.
splines의 단점은 예측 변수의 외부 범위(outer range)에서 큰 분산을 가진다는 것이다($X$가 매우 작거나 큰 값을 가지는 경우).
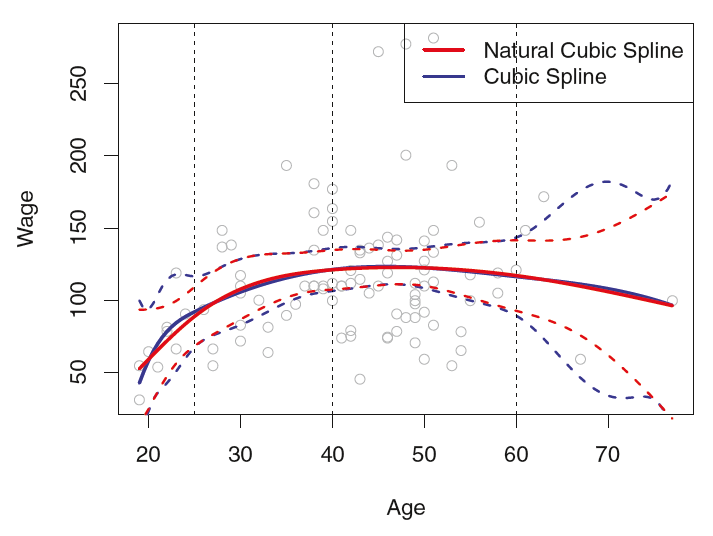
Figure 2는 급여(Wage) 데이터에 3개의 knots을 가지는 Cubic splines, Natural cubic splines을 적합시킨 것이다. 그림에서 보다시피 cubic splines의 경우 boundary region($X$의 양 끝)에서 신뢰구간이 다소 넓게 추정되고 있다. A natural splines는 이를 보완하기 위해 regression splines에 추가적인 boundary constraints(제약)을 준 모형으로 boundary에서 더 안정적인 추정을 제공한다(신뢰 구간이 더 좁아짐).
지금까지 배운 모형을 간략하게 정리하면 다음과 같다
| 기저 함수를 이용한 모델링 | 방식 |
| Piecewise polynomial | Piecewise constant regression + 다항 회귀 |
| Continuous piecewise polynomial | Piecewise polynomial + Knots에서 연속성 제약 |
| A degree-d Splines | piecewise regression + Knots에서 연속성 제약 + (d-1)차수까지의 미분 계수에 대한 연속성 제약 |
| Natural spline | Splines + Boundary에서 선형성(linearity) 제약 |
Knots의 수와 위치 결정
spline을 적합할 때 knots의 수와 위치를 결정하는 것은 필수적이다. regression spline은 knots이 많은 지역에서 가장 flexible하다. 이러한 이유로, knots을 두는 한 가지 방법으로는 데이터의 패턴이 급격하게 변하는 지역에는 knots을 많이 두고, 안정적인 지역에는 knots을 적게두는 방법이 있다. 이 방법은 실제로도 꽤 잘 작동한다.
knots을 두는 가장 간단한 방법은 $X$의 범위에 균일하게 배치하는 것이다. 이를 위해선, 원하는 자유도를 명시하고 software(e.g. R, Python)가 해당 자유도 만큼 데이터의 uniform quantiles에 knots을 두도록 하면 된다.
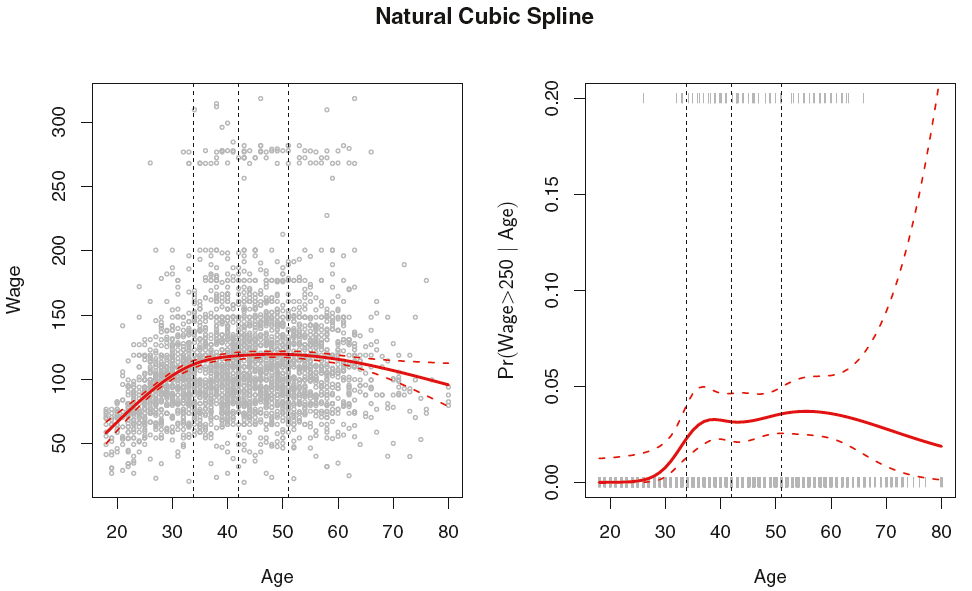
Figure 3의 왼쪽 그림은 나이를 $X$ 급여(단위 : 1000달러)를 $Y$로 natural cubic spline을 적합한 것이며, 오른쪽 그림은 로지스틱 회귀모형을 이용하여 급여가 250이 넘는 경우 $Y=1$로 코딩하여 나이가 주어졌을때 급여가 250이 넘을 사후확률을 모델링하는데, 이때 로짓을 선형으로 고려하는 것이 아니라 Natural Cubic spline을 고려한 경우이다. Knots은 R에 자유도 4를 명시하여 uniform quantiles에 knots을 자동으로 배치하도록 했다. 위 모형의 자유도로 4인 이유는 사실상 knot이 3개인 것으로 보이지만, 2개의 boundary knots이 존재하여 총 5개의 knots을 갖는다. 5개의 knots을 갖는 cubic splines은 자유도가 9이며, 이때 natural splines은 각 boundary에서 2가지 추가적인 natural constaints를 가지므로 총 자유도는 9-4=5가 된다. 이때 해당 자유도에 절편(intercept)에 속하는 상수가 포함되어있어 결국 위와 같은 natural cubic splines의 자유도는 4가 되는 것이다.
spline의 knots의 갯수 또는 자유도를 결정하는 또 하나의 합리적인 방법은 교차 검증(Cross-validation)을 이용하는 것이다. 다음은 10-fold CV를 이용하여 Natural cubic spline과 cubic spline의 자유도에 따른 MSE의 변화를 살펴본 것이다.

두 모형 모두 결과가 거의 유사하며, Natural cubic spline의 경우 자유도 3, Cubic spline의 경우 자유도 4가 적절해 보인다.
다항 회귀와 regression splines의 비교
regression splines는 종종 다항 회귀(Polynomial regression)보다 훨씬 더 우수한 결과를 제공한다. 이는 차수를 높혀야(자유도가 커짐) flexible한 적합을 보여주는 다항 회귀와는 달리, splines의 경우 차수는 고정(자유도는 유지)하면서 knots의 수를 늘려 곡선을 더 flexible하게 만들 수 있기 때문이다. 그래서 일반적으로 splines이 더 안정적인 추정량을 제공한다. 다음의 Figure 5는 자유도가 15인 natural cubic spline, 다항 회귀를 비교한것이다.
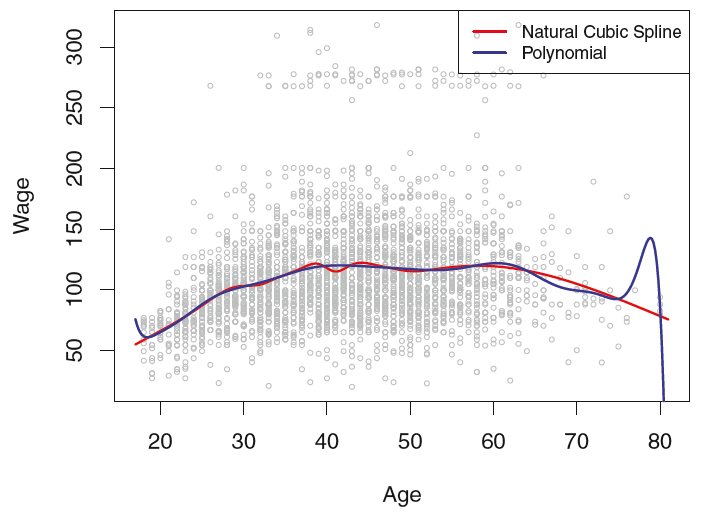
다항 회귀의 경우 boundary에서 지나친 flexibility로 인해 좋지 않은 추정 결과를 보이는 반면, natural cubic spline의 경우 boundary region에서도 합리적인 적합 결과를 보여주고 있다.
참고 문헌
James, Gareth, et al. An Introduction to Statistical Learning. Springer. 2013
'Machine&Statistical Learning > GAM' 카테고리의 다른 글
| GAMs: Generalized additive models (3) | 2020.06.22 |
|---|---|
| Local regressions (0) | 2020.06.10 |
| Smoothing splines (0) | 2020.06.09 |
| 다항 회귀와 계단 함수 (0) | 2020.06.08 |
| 선형모형의 한계 (0) | 2020.06.06 |




댓글