❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
※ prerequisites
국소 회귀(Local regressions)는 이제까지 봤던 splines처럼 flexible한 non-linear functions을 적합하는 것과는 조금 다른 접근으로, target point $x_0$ 근처의 관측치만을 이용하여(가까울수록 큰 가중치를 부여) 곡선의 적합을 수행해나간다. 다음의 그림은 국소 회귀의 이러한 기본적인 아이디어를 잘 보여준다.

그림의 파란색 곡선은 데이터를 발생시킨 함수를 나타내며, 밝은 오렌지색 곡선이 국소 회귀모형을 통해 추정한 함수이다. 오렌지색 점이 해당 영역(이를 span이라고 함)의 target point $x_0$를 의미하고, 종 모양의 노란색 영역은 span내의 각 점에 부여되는 가중치(weights)를 나타낸다. target point와 가까울수록 가중치가 커진다. 국소 회귀의 점 $x_0$에서 적합값 $\hat{f}(x_0)$는 그림처럼 weighted linear regression model(선형이 아닌 constant나 quadratic regression을 고려할 수 도 있음)을 적합하고 이에 $x_0$를 대입함으로 써 얻을 수 있다(그림의 오렌지색 점). 여기서 알 수 있는 바는, 가중치 $K_{i0}$는 target point에 따라 다르다는 것이다. 즉, 새로운 target point에 국소 회귀를 적합하기 위해서는 새로운 가중치 집합을 기반으로 least squares를 최소화시키는 새로운 weighted least squares regression model을 적합시켜야 한다. 이러한 이유로 국소 회귀를 "memory-based procedure"라고 부르기도 하는데, 이는 K-NN(Nearest neighbors)과 마찬가지로 예측을 수행할 때마다 결국 모든 training set이 필요하기 때문이다.
그림을 통해 국소 회귀모형을 적합시키는 과정을 대략적으로 알아보았는데, 이제 조금 더 자세히 알아보자. 국소 회귀모형의 적합을 위해서는 Weighting function $K$를 어떻게 정의할지, 그리고 linear, constant, quadratic regression 중에 어떤 모형을 적합할지 등과 같이 많은 선택이 필요하다. 이런 선택들 가운데 가장 중요한 것은 span($s$)의 선택이다. span은 smoothing splines의 $\lambda$와 같은 역할을 하며, span이 작을수록 모형은 더 local해지며 그에따라 매우 꾸불꾸불한(wiggly, 다르게 말하면 복잡한) 곡선이 만들어진다. span을 매우 크게 해서 training set 전체를 local 하나로 보고 전체에 적합되는 곡선을 만들 수도 있다. 이때 $s$의 선택은 마찬가지로 교차 검증(Cross-validation)을 통해 경험적으로 이루어진다. 다음의 그림은 이제까지 사용했던 급여(Y : Wage) 데이터에 각각 span을 $s = 0.7$, $s = 0.2$로 하는 local regression을 적합한 결과인데, 예상했던 바와 같이 $s=0.7$인 경우 더 smooth한 곡선이 만들어진다.
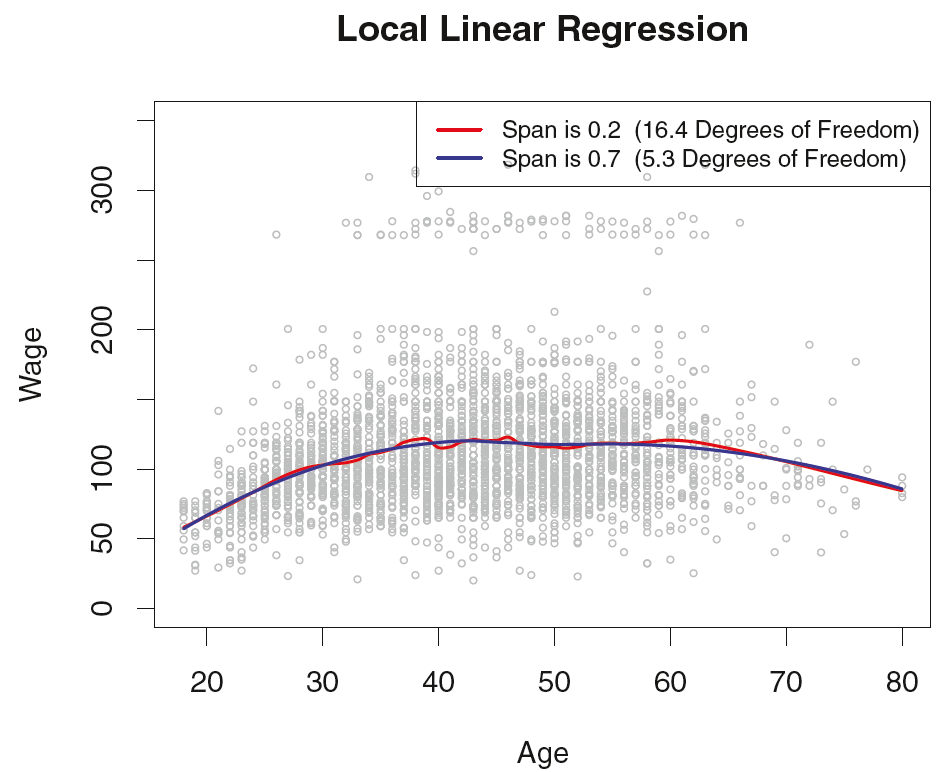
마지막으로, 국소 회귀의 단점을 언급하며 글을 마친다. 국소 회귀를 적합시킬 데이터의 $p$(고려할 features의 갯수)가 3 또는 4보다 클 경우 매우 좋지 못한 성능을 보인다. 그 이유는, $p$가 3 또는 4보다 큰 차원에서는 일반적으로 $x_0$ 근처에서는 관측치가 몇 개 존재하지 않기 때문이다.
참고 문헌
James, Gareth, et al. An Introduction to Statistical Learning. Springer. 2013
'Machine&Statistical Learning > GAM' 카테고리의 다른 글
| GAMs: Generalized additive models (3) | 2020.06.22 |
|---|---|
| Smoothing splines (0) | 2020.06.09 |
| Regression splines (0) | 2020.06.08 |
| 다항 회귀와 계단 함수 (0) | 2020.06.08 |
| 선형모형의 한계 (0) | 2020.06.06 |




댓글