❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
※ prerequisite
Bias reduction of Lasso estimator
이번 글에서는 목적함수에 Ridge의 penalty term을 추가하여 Lasso 추정량의 Variance를 줄이는 방법들에 대해 소개한다. Variance를 줄이는 접근 방법을 소개하는 이유는 정확한 추정량을 얻기위해 Variance reduction을 통해 얻는 이득이 Bias가 늘어나는 비용보다 더 크기 때문이다.
1. Elastic net
$Q(\boldsymbol{\beta} | X, \boldsymbol{y}, \boldsymbol{w}) = \frac{1}{2}\left \| \boldsymbol{y} - X\boldsymbol{\beta} \right \|^2 + P_{\lambda}(\boldsymbol{\beta})$, where $P_{\lambda}(\boldsymbol{\beta}) = \lambda_1\left \| \boldsymbol{\beta} \right \|_1 + \frac{\lambda_2}{2}\left \| \boldsymbol{\beta} \right \|_2^2$
Elastic net은 위와 같이 Lasso 회귀에 Ridge penalty를 추가한 형태의 목적함수를 가진다. Lasso의 해는 항상 uniqueness를 갖지 못한다(Lasso의 목적함수는 항상 convex를 보장받지 못하기 때문에). 그러나, 항상 유일한 해를 갖는 Ridge regression의 penalty term을 추가함으로써, Elastic net은 Ridge 회귀 추정량의 uniqueness와 proportional shrinkage(비율적 축소) 성질을 상속(inherit)받게 된다.
(1) Reparameterization
Elastic net의 Reparameterization은 $\lambda$ 관점의 regularization 모수 $\alpha$로 표현된다:
$\lambda_1 = \alpha\lambda$ , $\lambda_2 = (1-\alpha)\lambda$
이를 통해 $\alpha$를 고정하면 $\lambda$만 조절해서 Tuning을 수행할 수 있으므, 실제 문제에서 유용하다.
(2) Orthonormal case
$X^TX$를 정규직교 행렬(orthonormal matrix)로 가정하면 Elastic net penalty가 회귀계수 추정량에 미치는 효과를 직관적으로 알 수 있다.
$\hat{\beta}_j = \frac{S(z_j | \lambda_1)}{1+\lambda_2}$
Elastic net의 penalty는 Lasso의 해를 추가적인 Ridge penalty로 축소하는 역할을 한다. Ridge 회귀는 추정량을 0에 가깝게 축소하여 bias를 키우고, 분산을 낮춘다. 그러나, 실제 데이터의 추정에서 Bias가 Variance보다 우위에 있을 때가 있으므로, Ridge penalty를 추가하는 것이 항상 이점을 가져다주는 것은 아니다.
(3) Grouping effect
Grouping effect는 서로 상관이 큰 변수 간에 비슷한 회귀계수 추정량을 가지게 되는 것으로, Elastic net의 추정량이 가지는 성질 중 하나에 해당한다. 많은 고차원 데이터는 서로 상관이 큰 예측변수들을 포함하며, 이때 Elastic net이 가지는 두 성질 Shrinkage와 Grouping effect는 효과적인 해결책이 된다.
Grouping effect는 수식으로 다음과 같이 두 변수의 회귀계수 추정량의 차이에대한 상한값으로 표현할 수 있다:
$|\hat{\beta}_j - \hat{\beta}_k| \leq \frac{\left \| \boldsymbol{y} \right \| \sqrt{2(1-\rho_{jk})}}{\lambda_2\sqrt{n}}$, where $\rho_{jk}$ is the sample correaltion between $\boldsymbol{x}_j$ and $\boldsymbol{x}_k$
$\rho \rightarrow 1$일수록, $\hat{\beta}_j$와 $\hat{\beta}_k$간의 차이는 0에 수렴한다.
○ Simulation study
Grouping effect를 확인하기 위해 Simulation study를 수행한다. $n = 50$, $p = 100$인 데이터를 고려할 것이며, 모든 변수는 marginal로 표준정규분포를 갖고 변수 간에는 다음의 두 종류의 상관(correlation)이 존재한다고 가정한다.
① Compound symmetric : 모든 변수가 pairwise로 상관계수 $\rho$를 가진다.
② Block diagonal : 100개의 변수가 5개씩 블록을 형성하고, 각 블록 내에서 pairwise로 상관계수 $\rho$를 가지며 블록 간의 독립이다.
True 모형으로는 $\beta_1 = \beta_2 = \cdots = \beta_5 = 0.5$, $\beta_6 = \beta_7 = \cdots = \beta_{100} = 0$을 고려한다.
Simulation 결과에서 주목할만한 점은 Block diagonal에서 Elastic net의 grouping effect가 드러난다는 것이다. 또한, 이 실험에서 Elastic net의 $\lambda$ 선택은 $\lambda_1 = \lambda_2$로 두고 독립적인 validation set을 통해 이루어졌다.

왼쪽은 Compound symmetric, 오른쪽은 Block diagonal로 두 경우 모두 변수 간의 상관이 크지 않으면 lasso와 Elastic net의 추정량의 정확도에 큰 차이는 없다. 오히려 상관이 0에 가까울 때는 Lasso가 더 정확할 때도 있다. 그러나, 변수 간의 상관이 큰 경우 Elastic net은 Lasso보다 훨씬 더 좋은 추정을 하며, 이는 회귀계수들이 grouping property를 가지는 Block diagonal에서 훨씬 더 잘 드러난다. 실제로 grouping effect는 Elastic net penalty를 이용하는 큰 motivation 중 하나이다.
2. SNet과 MNet(Non-convex penalty + Ridge penalty)
MCP와 SCAD의 목적함수는 non-convex로 local minima(minima are plural of minimum)가 존재한다. 이는 최적화에 어려움을 초래하고 수치적 안정성을 떨어뜨린다. 이때 우리는 strictly convex인 Ridge penalty를 함께 추가함으로써 상당한 안정화를 가져올 수 있다. 이렇게 non-convex penalty에 Ridge penalty를 결합하는 것은 Ridge penalty를 추가하는 것의 가장 큰 motivation에 해당한다.
Elastic net에서처럼 Ridge 추정량 $\lambda_2$는 MCP와 SCAD 추정량을 축소하는 효과를 가진다. 예를 들어, Orthonormal case에서 MCP에 대한 Ridge 추정량의 효과는:
$\hat{\beta}_j = \left\{\begin{matrix}
\frac{z_j}{1+\lambda_2} &, |z_j| > \gamma\lambda_1(1+\lambda_2)\\
\frac{S(z_j|\lambda_1)}{1-\frac{1}{\gamma} + \lambda_2} & |z_j| \leq \gamma\lambda_1(1+\lambda_2)
\end{matrix}\right.$
SCAD는 좀 더 복잡하지만, MCP와 비슷한 형태를 띤다. $\lambda_2$는 shrinkage 역할을, $\gamma$는 반대로 bias를 줄이는 역할을 하고 있다. $ |z_j| \leq \gamma\lambda_1(1+\lambda_2)$의 경우엔 $\lambda_2$와 $\gamma$가 동시에 존재하여 서로 cancel-out이 된다. 그러나, 이는 Orthonormal case에만 해당하는 것이며 그 외에 $\lambda_2$와 $\gamma$의 역할은 cancel-out 되지 않는다. 특히, 변수 간의 상관이 큰 경우엔 서로 조금 다른 역할을 한다. 이는 앞으로 수행할 Simulation study와 Case study에서 실제로 확인할 수 있다.
3. Simulation study
Lasso, MCP, Elastic net, MNet의 추정 정확도 비교를 위한 Simulation study를 진행한다.
(1) Independent case
{$x_j$}들은 독립적인 표준정규분포를 따르며, $\boldsymbol{y}$는 다음과 같은 분포를 따른다.
$\boldsymbol{y} = X\boldsymbol{\beta} + \epsilon, \; \epsilon \sim N(0, 1) $
데이터 구조는 $n = 100$, $p = 500$, 12개의 non-zero 회귀계수를 True 모형으로 고려했다. 또한, 데이터 생성 과정에서 Signal(s)은 0.1부터 1.1까지 고려하였다.
모든 방법론의 Tuning 모수들은 $n=100$인 독립적인 validation set에 대한 MSPE(Mean squared prediction error)를 기반으로 선택되었다. Lasso와 MCP는 $\lambda$만을 Tuning했다(MCP $\gamma = 3$ 고정). MNet은 먼저 고정된 $\alpha$에 대해 최적의 $\lambda$를 찾고(하단의 좌측 그림), 후에 ENet과 Mnet 각각의 $\lambda$와 $\alpha$의 2차원 grid를 고려하여 최적의 조합을 선택했다(하단의 우측 그림). 실험 결과는 다음과 같았다:
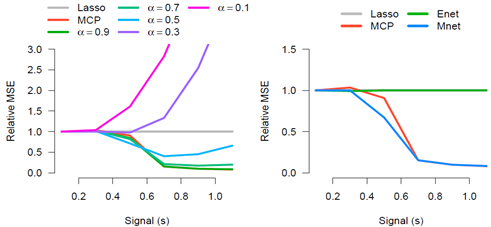
Signal($s$)의 변화에 따른 Lasso 추정량의 MSE 기준으로 상대적인 MSE의 변화를 나타낸 그래프이다. 먼저 왼쪽 그림을 보자. $s$가 작은 경우($R^2$가 작은 데이터)에는 모든 모형이 결국 $\hat{\boldsymbol{\beta}} \approx 0$으로 추정하기 때문에, 모두 비슷한 패턴을 보인다. $s$가 커짐에 따라 MCP는 MNet의 $\alpha = 0.9$와 함께 가장 정확한 추정량이 된다($\alpha = 0.9$를 고려하면 Ridge penalty가 매우 작아짐).
이제 $\alpha$도 변수로 함께 고려한 오른쪽 그림을 살펴본다. 이때 Lasso와 ENet은 거의 차이가 없다. 특히 $s$가 클 때는 $\alpha \approx 1$로 Ridge penalty는 거의 존재하지 않았기 때문에, 두 추정량이 같다고 볼 수 있다. MCP와 MNet은 $s$가 작은 경우 Lasso, ENet과 비슷하게 움직이지만, $s$가 커짐에 따라 훨씬 더 좋은 성능을 보여준다.
Independent case의 Simulation study의 결과는 변수들이 독립일 때는 Ridge penalty의 추가로 큰 이득을 보긴 어렵지만, 추정의 정확도를 개선할 수 있음을 나타낸다.
(2) Correlation case
Ridge penalty의 효과를 좀 더 직접적으로 확인하기 위해, 변수간 상관에 극단적인 가정을 한다. {$x_j$}들은 pairwise로 $\rho = 0.7$의 상관을 가지며, marginal로 독립적인 표준정규분포를 따른다. 이 외의 조건은 Independent case와 같다.
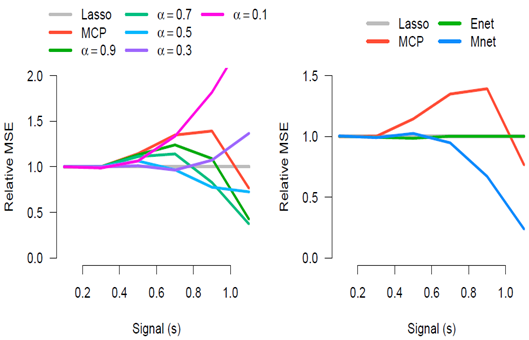
Correlation case에서는 Ridge penalty를 통한 shrinkage의 효과가 훨씬 더 크게 드러난다. 예를 들어, Independent case에서는 MCP가 최적의 추정량과 멀리 떨어진 경우가 없었지만, Correlation case의 경우 $s$가 커지면 상당히 좋지 않은 성능을 보인다. 또한, Independent case에서 MCP와 MNet의 성능은 거의 비슷했지만, 여기서는 MNet이 훨씬 더 훌륭한 추정을 수행한다.
즉, Independent case의 경우 Ridge penalty 추가를 통해 얻을 수 있는 개선점이 거의 없지만, correlation이 존재하는 경우 상당한 개선 효과를 가져다준다. $\alpha$의 최적값은 정해져 있지 않으며 교차 검증을 통한 경험적(empirical) 선택이 필요하다.
4. SNet과 Mnet의 목적함수 Convex 조건
Lasso 회귀에 Ridge penaty를 추가한 Elastic net은 Ridge 추정량의 uniqueness를 상속(inherit)받게 되어, 항상 Convex 형태의 목적함수를 가지게 된다. 그러나, non-convex penalty의 경우 다음의 조건이 필요하다:
$\left\{\begin{matrix}
\gamma > \frac{1}{1+\lambda_2}, & MCP\\
\gamma > 1 + \frac{1}{1+\lambda_2}, & SCAD
\end{matrix}\right.$
즉, Ridge penalty를 증가시킬수록 SCAD와 MCP의 목적함수는 convex에 가까워진다. 일반적인 non-orthonormal case의 경우 위 식에서 분모의 1을 $c_{min}$($X^TX$의 최소 고윳값)으로 바꿔주면 된다. Lasso의 Bias reduction에 관한 방법론의 경우 $\gamma$를 증가시켜 목적함수의 안정성을 유지하고 불연속(discontinuous) 함수로 수렴하는 것을 막을 수 있었는데(Bias reduction of Lasso estimator - Folded concave penalties의 thresholding에 관한 부분 참고), SNet과 MNet에서는 Ridge component $\lambda_2$를 조절하여 이뤄낼 수도 있다(즉, $\alpha$의 조절을 통해).
5. Case study
$\lambda_2$를 조절하는 것의 효과를 실제로 확인해보기 위해 Case study를 진행한다.
(1) 유방암 유전자 표현(gene expressions) 연구
유방암 환자들의 유전자 표현(expression) 데이터를 이용해 Elastic Net과 MNet의 예측 정확도와 선택한 변수 개수를 $\alpha$에 따라 비교한다.

$\alpha$에 무관하게 두 방법론에서 전반적인 예측력($R^2$)은 매우 비슷하지만, 선택된 변수들은 꽤 다르다. 두 모형 모두 $\alpha$가 작아짐에 따라($\lambda_2$의 비율이 커질수록), 선택된 변수의 수가 많아지고 있다. 우리가 기대했던 결과와 다르게 나온 이유는 오른쪽 그림에서 확인할 수 있듯이 해당 데이터에 강한 상관이 존재하지 않기 때문이다(Simulation study의 Independent case와 비슷한 상황). 유방암 데이터는 실제로 유전자 간 pairwise 상관계수의 크기 99%가 0.4를 넘지 못한다.
(2) 쥐 망막에 관한 유전자 표현 연구
이번 데이터는 변수 간의 상관이 커서, Ridge penalty의 효과를 확실하게 보여줄 수 있을 것이다. 쥐의 망막에 문제를 일으키는 병에 대한 유전자 표현 데이터를 이용할 예정이며, 표본으로 나이가 12주인 남자 쥐 120마리의 눈 조직을 채취했다. 또한, 유전자의 개수는 총 18,975개로 variable screening을 통해 분산이 가장 큰 5,000개만을 분석에 이용했다.
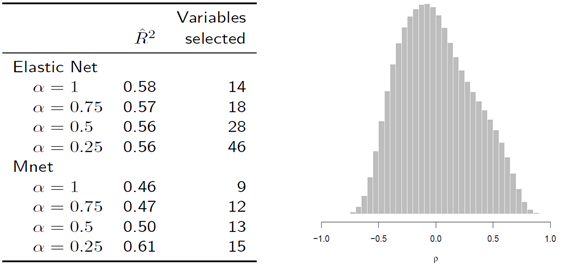
오른쪽 그림에서 확인할 수 있듯이 변수 간 상관이 매우 크기 때문에 Ridge penalty의 추가로 더 간단하면서 정확한 예측 성능을 가진 모형을 적합할 수 있을 것이다. 왼쪽 표의 실제 결과를 보면, 유방암 연구에서는 잘 드러나지 않았던 Ridge penalty를 추가한 것의 효과는 상당한 영향력을 보여준다. 먼저 $\alpha = 1$일 때, 즉 Lasso와 MCP를 비교해보면 오히려 MCP가 더 좋지 못한 예측 정확도를 보여준다. 그러나, $\alpha$를 감소시켜 Ridge penalty의 비율을 늘려감에 따라 MNet이 Elastic Net보다 훨씬 더 적은 개수의 변수로 더 좋은 예측 성능을 낼 수 있게 된다. Lasso에서 Ridge penalty의 결합은 더 dense한 모형을 생성하는데, 그에 따라 얻는 예측 성능의 이득은 딱히 없어 보인다. $\alpha = 0.25$인 MNet 모형은 아주 훌륭한 결과를 보여준다.
5. 벌점 회귀의 이론적 특성
벌점 회귀를 통해 추정된 회귀계수가 가지길 바라는 이상적인 이론적 특성들을 소개한다.
(1) 추정(Estimation)
$\left \| \hat{\boldsymbol{\beta}} - \boldsymbol{\beta}^* \right \|$, where $\boldsymbol{\beta}^*$ : True value
추정량이 실제 $\boldsymbol{\beta}$ 값에 최대한 근접하길 바란다.
(2) 예측(Prediction)
$\frac{1}{n} \left \| X\hat{\boldsymbol{\beta}} - X\boldsymbol{\beta}^* \right \|^2$, where $\boldsymbol{\beta}^*$ : True value
우리의 모형이 정확한 예측 결과를 낼 수 있기를 바란다. 참고로 $\hat{\boldsymbol{\beta}} \approx \hat{\boldsymbol{\beta}}^* \Rightarrow X\hat{\boldsymbol{\beta}} \approx X\boldsymbol{\beta}^*$는 성립하지만, 역은 성립하지 않는다. 그 이유는 추정의 일치성보다 예측의 일치성이 더 약한 조건에서(under weaker conditions) 발생하기 때문이다.
(3) 변수 선택(Variable selection)
sparse 모형에서는 변수 선택의 효과도 있기를 기대한다. 이를 측정하는 다른 몇몇 방법이 있는데, 그중 하나는 부호 일치성(sign consistency)이다:
$sign(\hat{\beta}_j) = sign(\beta_j^*)$ with high property
$sign(x)$는 부호 함수로 $x$가 양의 실수면 1, 0이면 0, 음의 실수면 -1을 반환한다. 이 속성은 달성하기 가장 어려운 특성에 해당한다. 그 이유는 $\hat{\beta}_j$와 $\beta_j^*$의 값이 매우 비슷한 상황에서 하나는 0, 다른 하나는 0에 매우 가까운 non-zero quantity로 추정은 매우 근사하게 해냈지만, 결국 다른 부호를 가지기 때문이다.
참고 자료
High-Dimensional Data Analysis (Patrick Breheny)
'고차원 자료분석' 카테고리의 다른 글
| Penalized robust regression (0) | 2020.06.02 |
|---|---|
| Penalized logistic regression (0) | 2020.06.02 |
| Bias reduction of Lasso estimator (2) | 2020.05.26 |
| Lasso regression (0) | 2020.04.28 |
| Ridge regression (1) | 2020.04.10 |




댓글