❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
※ prerequisite
고차원 데이터에 대한 회귀분석에서 $\boldsymbol{\beta}$에 대한 ML 추정량(OLS 추정량)은 많은 결점이 발생한다. 이를 해결하기 위해서는 변수선택(variable selection 또는 model selection)을 통한 차원의 축소가 필요로 되는데, 변수선택과 추론을 같은 데이터로 수행하는 Post-selection OLS 모형을 고려하면 ML 추정량이 갖는 좋은 추론적 특성들을 잃게 된다. 그래서 고차원 데이터의 회귀분석에 근본적인 해결책으로 벌점 회귀(Penalized regression)의 한 종류 “Ridge regression”에 대해 소개한다. 앞으로의 설명에서는 편하게 Ridge라고 칭한다. 우리가 알아볼 내용을 크게 7가지로 나눠 요약하고, 자세한 설명을 하려고 한다.
○ 고전적인 선형회귀 모형과 Ridge의 목적함수를 정의하고, Ridge penalty가 어떻게 OLS 추정량의 크기를 줄이는 역할을 하는지를 알아본다.
○ Ridge 추정량이 가지는 장점에 대해 알아본다. 고차원 데이터에서는 회귀계수 추정에 불안정을 안겨주는 다중공선성(multicollinearity) 문제가 발생할 가능성이 크다. 이때 Ridge는 매우 효과적인 접근방법이며, 이를 Simulation study를 통해 직접 보인다.
○ 회귀계수 추정에 대한 MSE를 정의하고 Ridge 추정량과 OLS 추정량을 비교한다. 결과부터 말하면 Ridge는 항상 다음을 만족하는 $\lambda$가 존재한다.
$MSE(\hat{\beta}_{\lambda}) < MSE(\hat{\beta}^{OLS})$
○ OLS 추정량과 Ridge 추정량의 기하학적인 이해
○ Ridge를 베이지안의 관점에서 설명하고, likelihood based methods와의 추론적 특성의 차이를 알아본다.
○ Ridge에서 $\lambda$의 선택에 대해 알아보고, 몇 가지 평가 기준을 제시한다.
○ 실제 데이터를 통해 $\lambda$값 선택의 중요성을 강조하기 위해, $\lambda$에 따른 회귀계수 추정값들의 변화를 살펴본다.
1. OLS와 Ridge의 목적함수 비교
본격적인 설명에 들어가기 전에 이 글에서 기호 $L$은 음의 로그가능도함수(negative log-likelihood)를 나타냄을 기억하자. 굳이 음을 취하는 이유는, MLE에서는 가능도함수를 최대화하는 모수를 구하는데 이를 최소화하는 문제로 바꿔 손실함수(loss function)로 다루기 위함이다. 먼저 OLS의 손실함수를 정의한다.
$L(\theta | \textrm{Data}) = -\textrm{log}\;l(\theta|\textrm{Data}) = -\textrm{log}\;p(\textrm{Data} | \theta)$
선형회귀에서는 $y$(또는 오차항이라고 표현해도 됨)에 대해 정규분포를 가정하므로 loss function을 다음과 같이 정리할 수 있다.
$L(\boldsymbol{\beta}|\boldsymbol{X}, \boldsymbol{y}) = \frac{n}{2}\textrm{log}(2\pi\sigma^2) + \frac{1}{2\sigma^2}\sum_i (y_i - \boldsymbol{x}_i^T\boldsymbol{\beta})^2$
이때 MLE를 찾는 목적에서 분산을 상수취급하면 첫번째 항은 $\beta$와 무관하므로, 결국 loss function은 다음과 같이 써진다.
$L(\boldsymbol{\beta}|\boldsymbol{X}, \boldsymbol{y}) = \frac{1}{2\sigma^2}\sum_i (y_i - \boldsymbol{x}_i^T\boldsymbol{\beta})^2$
고차원 데이터에서 likelihood based method로 회귀계수 추정을 진행할 경우, 문제점을 가진다. 그래서 이를 해결하기 위해 약간의 수정을 하여 다음과 같이 새로운 목적함수를 정의하자:
$Q(\beta | \boldsymbol{X}, \boldsymbol{y}) = L(\beta | \boldsymbol{X}, \boldsymbol{y}) + P_{\lambda}(\boldsymbol{\beta})$
($P$ : Penalty term, $\lambda$: regularization의 역할을 하는 모수)
$Q$가 바로 Penalized regression의 목적함수(Objective function)이다. Ridge는 penalty term으로 squared $l2$-norm을 사용한다:
$P_{\tau}(\boldsymbol{\beta}) = \frac{1}{2\tau^2}\sum_{j=1}^p \beta_j^2$
($\tau^2 = \frac{\sigma^2}{\lambda}$)
그래서 Ridge의 목적함수는 다음과 같이 정리할 수 있다.
$Q(\beta | \boldsymbol{X}, \boldsymbol{y}) = \frac{1}{2\sigma^2}\sum_i (y_i - \boldsymbol{x}_i^T\boldsymbol{\beta})^2 + \frac{1}{2\tau^2}\sum_{j=1}^p \beta_j^2$
표현의 간소화를 위해 $\sigma^2$을 곱해주면:
$Q(\beta | \boldsymbol{X}, \boldsymbol{y}) = \frac{1}{2}\sum_i (y_i - \boldsymbol{x}_i^T\boldsymbol{\beta})^2 + \frac{\lambda}{2}\sum_{j=1}^p \beta_j^2$ ($\because \lambda = \frac{\sigma^2}{\tau^2}$)
선형회귀에서 Ridge penalty를 줄 경우, $\beta$의 ML 추정에 closed form(닫힌 형태)을 제공해주어 매우 편리하다(닫힌 형태가 아니면 수치해석적 접근이 필요함).
$\hat{\boldsymbol{\beta}} = (\boldsymbol{X}^T \boldsymbol{X} + \lambda \boldsymbol{I})^{-1} \boldsymbol{X}^T\boldsymbol{y}$
위 식이 Ridge 추정량이며 $\lambda$를 성분으로 하는 대각행렬의 역행렬이 더해졌을뿐, OLS 추정량과 매우 비슷하다. Ridge penalty의 효과를 이해하기 위해, design matrix $\boldsymbol{X}$를 직교행렬로 가정하자.
$\hat{\beta}_j = (\boldsymbol{X}^T \boldsymbol{X} + \lambda \boldsymbol{I})^{-1} \boldsymbol{X}^T\boldsymbol{y} \\ \;\;\;\; = (1+\lambda\boldsymbol{I})^{-1}\boldsymbol{X}^T\boldsymbol{y} \\ \;\;\;\; = \frac{1}{1+\lambda}\boldsymbol{X}^T\boldsymbol{y} \\ \;\;\;\; = \frac{1}{1+\lambda}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} \\ \;\;\;\; = \frac{\hat{\beta}_j^{\textrm{OLS}}}{1+\lambda}$
직교행렬을 가정하였으므로, $\boldsymbol{X}^T\boldsymbol{X} = \boldsymbol{I}$가 되어 위와 같이 정리가 된다. 변수 $j$의 Ridge 추정량은 결국 변수 $j$의 OLS 추정량을 $(1+\lambda)$만큼 나눠 그 크기를 줄인 형태가 된다. 이는 Ridge의 본질적인 특성이다. 또한 이러한 이유에서 Ridge와 Lasso를 모두 포함한 Penalized regression을 Shrinkage methods라고 표현하기도 한다(i.e. ridge penalty를 적용하는 것의 주된 효과는 추정량을 0을 향해 축소(shrink)시키는 것이다).
마지막으로 언급하고 싶은 점은 Ridge regression 적합 시 변수들의 단위가 다른 경우이다. 각 변수의 단위가 다르면, 회귀계수의 크기는 이에 의존할 수밖에 없다(단위가 큰 변수는 중요한 변수여도 회귀계수 크기가 작게 추정됨). 그런데 Ridge에서는 중요하지 않은 변수일 수록 회귀 계수의 크기가 0에 가깝게 만들어 버린다. 그래서 중요한 변수임에도 단위가 크다는 이유로 회귀계수의 크기가 작아져 중요도가 떨어지는 변수로 오해하는 상황이 생길 수 있다. 그래서 변수의 단위에 차이가 있는 데이터라면, 사전에 표준화를 진행하고 Ridge regression을 적합하는 것이 좋다. 표준화를 진행하여도 loss function에 끼치는 영향이 없다. $\boldsymbol{X}$의 위치 이동(location shift, 중심을 0으로 맞추는 것)은 intercept(절편) term에서 설명되고(intercept에 해당하는 $\beta_0$는 penalty에 포함되지 않는다), 척도화(scale, $\sigma^2$으로 나눠주어 단위를 맞춰주는 것)는 모형이 적합될 때 반영된다.
2. Ridge 추정량의 장점
Ridge는 다중공선성이 존재할 때 매우 효과적이다. 이를 simulation study를 통해 간단하게 확인하면:고차원 데이터에서는 회귀계수 추정에 불안정을 안겨주는 다중공선성(multicollinearity) 문제를 피하기 힘들다. Ridge는 이때 매우 효과적인 접근방법이다. 이를 simulation study를 통해 바로 확인해보자.

simulation study 수행을 위해 R 코드를 작성한 것이다. $X_1$은 $N(0,1)$로부터, $X_2$는 $N(X_1, 0.01^2)$로부터 각각 표본을 20개씩 발생시켜, 의도적으로 $X_2$가 $X_1$의 값에 의존하도록 다중공선성을 야기시켰다. 그리고 이때 고려한 True 모형은 $y = 3 + x_1 + x_2$이다. 고전적인 회귀 모형을 적합시킨 결과가 > lm(y ~ x1 + x2)의 아웃풋이며, Ridge를 적용시킨 결과가 마지막 코드의 Output이다. OLS의 계수 추정 결과는 $\beta_1 + \beta_2 = 2$를 맞추긴 했으나, True 모형과는 전혀 맞지 않는다. 그 이유는 아마 다중공선성의 존재로 $X^TX$의 역행렬이 존재하지 않아서(가능도 함수의 표면이 평평해짐), 무수히 많은 해가 존재하기 때문일 것이다. 추정량의 분산은 확인해보지 않았지만, 매우 클 것으로 예상한다. 그에 반면 Ridge는 매우 안정된 추정 결과를 보여주고 있으며, True 모형과 거의 일치한다.
다중공선성의 존재에도 Ridge가 매우 안정적인 추정을 하는 이유는 뭘까? $X$간에 다중공선성이 존재할 때 발생하는 OLS 추정의 문제점은 Ridge에서는 발생하지 않는다. 그 이유는 Ridge의 회귀계수 추정에 쓰이는 수정된(modified) ML 추정은 어떤 design matrix가 주어지더라도, $\lambda>0$이면 $(X^TX + \lambda I)$의 가역성을 항상 보장하기 때문이다. 따라서 Ridge는 항상 유일한 해 $\hat{\beta}$이 존재한다. 즉, simulation study의 결과는 우연한 결과가 아니다.
3. MSE를 통한 OLS 추정량과 Ridge 추정량의 비교
OLS와 Ridge의 $\boldsymbol{\beta}$ 추정량간의 비교는 Bias-Variance Tradeoff 관점에서도 할 수 있다. 모형의 regularization 관점에서 보면, 고전적인 회귀 모형(OLS)에는 Bias가 매우 작아져 데이터에 과적합 되는 문제를 조절할 수 있는 모수가 존재하지 않는다. 그러나 벌점 회귀에서는 $\lambda$를 통해 이를 조절할 수 있다. 이러한 이유로 목적함수의 정의에서 $\lambda$가 등장할 때, regularization 모수라고 정의한 것이다. 예를 들면, $\lambda \rightarrow 0$일수록 $\hat{\boldsymbol{\beta}}^{Ridge} \rightarrow \hat{\boldsymbol{\beta}}^{OLS}$가 된다. 앞서 정의했던 Ridge의 목적함수 식을 보면 당연한 결과임을 알 수 있다. 즉, $\lambda$를 줄일수록 Bias는 커지며 Variance는 작아진다. 통계학에서 모형 선택의 측도로 종종 고려하는 MSE는 사실 이 Bias와 Variance를 동시에 고려하는 측도이다. 그래서 $\hat{\boldsymbol{\beta}}$에 대한 MSE를 통해 OLS와 Ridge 추정량 간의 비교를 하고자 한다.
$MSE(\hat{\boldsymbol{\beta}}) = E\left \| \hat{\boldsymbol{\beta}} - \boldsymbol{\beta} \right \|$
Ridge는 앞서 언급했듯이 $\lambda$의 조절로 Regularization을 위한 “Bias-Variance Tradeoff”가 가능하다. 여기서 더 나아가서, Ridge가 가지는 놀라운 장점은 항상 다음을 만족하는 $\lambda$가 존재한다는 사실이다.
$MSE(\hat{\boldsymbol{\beta}}_{\lambda}) < MSE(\hat{\boldsymbol{\beta}}^{\textrm{OLS}})$

그래프의 회색 직선이 OLS 추정량의 MSE, 빨간색 직선이 Ridge 추정량의 MSE이다. 선형회귀에서의 ML 추정은 이론적으로 매우 훌륭한 특성들을 가지고 있지만, MLE를 0을 향해 축소함으로써 항상 더 나은 추정량을 얻을 수 있다는 것이다.
4. OLS 추정량과 Ridge 추정량의 기하학적인 이해

때로는 기하학적 접근이 직관적인 이해를 돕는다. 회귀계수 추정량의 변화에 따른 RSS(Residuals sum of squares) 값을 빨간색 등고선(contour)으로 나타냈으며, OLS 추정량이 그 최솟값에 해당한다(등고선 맨 안쪽의 점 $\hat{\beta}$). 이 점이 가장 작은 bias를 가지며, Training set에 과적합된 경우라고 할 수 있다. Ridge 추정시 제약을 기하학적으로 나타내면 그림처럼 원의 형태를 띤다. 이는 squared $l_2$-norm을 penalty로 쓰기 때문이다.
$\beta_1^2+ \beta_2^2 \leq c$
Ridge 추정량은 제약($c$ 값)의 크기에 따라 원의 크기가 결정되며, 이 원과 맞닿는 등고선의 가장 바깥쪽의 선이 Ridge 추정량이 된다. $c$ 값을 크게 키우면 어느 순간 OLS 추정량을 포함하게 되는데, 이는 $\lambda = 0$으로 설정한 결과와 동일할 것이다. 또한 Ridge의 제약은 기하학적으로 뾰족한 점이 없는 원의 형태를 띄기 때문에 등고선과의 교차점이 일반적으로 축 상에 나타나기 힘들다. 이 얘기는 Ridge는 회귀계수를 축소시키긴 하지만, 정확하게 0으로 수렴시키진 못함을 뜻한다. 즉, Ridge regression은 변수 선택의 목적까지는 충족시켜줄 수 없다.(Lasso를 이용하면 변수선택까지 진행이되며, 이는 다음 글로 포스팅할 예정이다).
5. Ridge의 베이지안 관점을 통한 해석
$\boldsymbol{\beta}$에 대한 사전분포로 $\beta_j \sim N(0, \tau^2)$을 가정하여(likelihood는 그대로 둠) $\boldsymbol{\beta}$의 사후분포를 유도하고, -log를 취해주면 Ridge 추정량의 목적함수와 정확하게 일치한다. 이를 증명해보자. 먼저 posterior를 구하는 식과 likelihood, $\boldsymbol{\beta}$의 $pdf$를 정의한다.
$p(\boldsymbol{\beta}|\boldsymbol{y}) = \frac{p(\boldsymbol{y}|\boldsymbol{\beta})p(\boldsymbol{\beta})}{p(\boldsymbol{y})} \propto p(\boldsymbol{y}|\boldsymbol{\beta})p(\boldsymbol{\beta})$ : posterior
$p(\boldsymbol{\beta}) = (\frac{1}{\sqrt{2\pi}\tau^2})^pe^{-\frac{1}{2\tau^2}\sum_{j=1}^p \beta_j^2}$ : prior
$p(\boldsymbol{y}|\boldsymbol{\beta}) = (\frac{1}{\sqrt{2\pi}\sigma^2})^ne^{-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i - \boldsymbol{x}_i^T\boldsymbol{\beta})^2}$ : likelihood
이제 posterior에 log를 씌워 정리하자.
$\textrm{log}\;p(\boldsymbol{\beta}|\boldsymbol{y}) \propto \textrm{log}\;p(\boldsymbol{y}|\boldsymbol{\beta}) + \textrm{log}\;p(\boldsymbol{\beta}) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = -n\textrm{log}\;(\sqrt{2\pi})-n\textrm{log}\sigma^2 - \frac{1}{2\sigma^2}\sum(y_i-\boldsymbol{x}_i^T\boldsymbol{\beta})^2 - p\textrm{log}(\sqrt{2\pi}\tau^2) - \frac{1}{2\tau^2}\sum\beta_j^2$
$\boldsymbol{\beta}$에 무관한 항은 삭제하자.
$\textrm{log}\;p(\boldsymbol{\beta}|\boldsymbol{y}) \propto - \frac{1}{2\sigma^2}\sum(y_i-\boldsymbol{x}_i^T\boldsymbol{\beta})^2 - \frac{1}{2\tau^2}\sum\beta_j^2$
Ridge 목적함수는 음의 로그가능도비를 기반으로 만들어졌기때문에, 위 식에 (-)를 취하고 $\sigma^2$을 곱하여 식을 간소화 하자.
$\textrm{log}\;p(\boldsymbol{\beta}|\boldsymbol{y}) \propto + \frac{1}{2}\sum(y_i-\boldsymbol{x}_i^T\boldsymbol{\beta})^2 + \frac{\lambda}{2}\sum\beta_j^2 = Q(\boldsymbol{\beta}|\boldsymbol{X}, \boldsymbol{y})$
즉, Ridge의 목적함수를 최소화하는 것은 $\boldsymbol{\beta}$의 사후분포의 기댓값(동시에 최빈값)을 찾는 것과 동일하며, 이는 MAP(Maximum a posteriori) 추정량으로 알려져 있다. 또한 이때 regularization parameter $\lambda$는 $\sigma^2/\tau^2$으로 정의되므로 사전분포의 정확도(precision, 분산의 역수 $1/\tau^2$)와 데이터가 가진 정보(likelihood의 분산 $\sigma^2$)의 비(ratio)라고도 할 수 있다. 하지만, Frequentist는 표본을 랜덤으로, 베이지안은 모수를 랜덤으로 가정한다. 따라서 추정량을 유도하는 식이 같다고 하더라도, 점 추정과 구간 추정의 추론과 해석은 각 관점에 따라서 달라지므로 주의해야 한다. 구간추정에 관한 차이점은 "구간추정 해석에 대한 고전적 관점과 베이지안 관점"을 참고하면 자세하게 이해할 수 있다. 점추정에 관한 차이만 짧게 이야기한다. 베이지안에서는 모수를 변수로 취급하기 때문에, $\beta$의 사후분포를 통해 추론을 하고 이는 연속형 분포에 해당하므로 $\beta = 0$일 확률은 0에 해당한다. 반면, Frequentist 관점에서는 모수를 상수로 취급하기 때문에, $\beta=0$에 대한 검정을 수행하는 것은 아주 의미있는 일이며 분석에서 흥미를 갖는 부분이기도 하다. 마지막으로 강조할 내용을 정리하고, 베이지안 관점에 관한 설명을 마친다.
- 앞서 Ridge를 베이지안 관점에서 해석하는 것을 보여주며, likelihood에서 penalty의 존재가 베이지안과 Frequentist간의 차이를 다소 흐릿하게 만들었을 수 있으나, penalized regression은 일반적으로 최대가능도 이론(Maximum likelihood theory)의 관점을 기반으로 하고 있다.
- penalized regression methods들의 연구 대부분은 주로 점추정과 그것의 특성에 포커스를 맞추고 있다. 그래서 베이지안과 Frequentist간의 추론적 차이에 관한 관점은 상대적으로 연구가 덜 진행된 부분이며, 이에 대한 추론적 방법을 개선시키는것은 현재 활발하게 연구되고 있는 부분이다.
6. $\lambda$의 선택
$\lambda$의 선택은 벌점 회귀 모형의 적합에 매우 중요한 점이며, 가장 뛰어난 예측력을 보여주는 값을 선택한다. RSS(Residual sum of squares)를 계산할 경우 모형의 예측 정확도를 과대추정하기 때문에, $y_i^{new}$와 예측 오차(PE:Prediction error)를 정의한다.
$y_i^{new} = f(\boldsymbol{x}_i) + \epsilon_i^{new}\;, \; E(y_i) = f(\boldsymbol{x}_i)$
$PE(\lambda) = \sum_{i=1}^{n}\left \{y_i^{new} - \hat{f}_i(\lambda) \right \}^2$
따라서 가장 뛰어난 예측력을 가지는 모형은 예측오차의 기댓값을 최소화하는 모형이다.
$E[PE(\lambda)] = E\sum_{i=1}^n \left \{ y_i^{new} - \hat{f}_i(\lambda) \right \}^2 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sum_{i=1}^n\left \{ y_i - \hat{f}_i(\lambda)\right \}^2 + 2\sum_{i=1}^n \textrm{Cov}\left \{ \hat{f}_i(\lambda), y_i\right \}$
예측 오차의 기댓값을 두 항으로 나눠서 볼 수도 있다. 두 항이 의미하는 바를 파헤쳐보자. 첫 번째 항은 within-sample fitting error, 두 번째 항은 within-sample fitting error에서 out-of-sample의 예측 오차를 과소평가하는 경향을 반영한 bias correction factor라고 보면 된다. 또한, 두 번째 항은 복잡도(complexity)의 측도 또는 자유도(degrees of freedom)로도 여겨진다. 즉, 예측 오차는 데이터에 대한 적합력과 동시에 모형 복잡도까지 고려하는 측도이다. 두 번째 항을 자유도 개념으로도 볼 수 있는 이유는, $\sum_{i=1}^n \textrm{Cov}\left \{ \hat{f}_i(\lambda), y_i\right \}$을 $y_i$의 분산인 $\sigma^2$으로 나누면 자유도를 계산하는 정의와 동일해지기 때문이다:
$\textrm{df} = \sum \frac{\textrm{Cov}(\hat{f}_i, y_i)}{\sigma^2} = \frac{ \textrm{tr} \left \{ \textrm{Cov}(\hat{\boldsymbol{f}}, \boldsymbol{y}) \right \} }{ \sigma^2 } $
OLS에서 자유도는 Design matrix $X$의 Rank와 같으며, Ridge의 경우 자유도는 다음과 같이 주어진다.
$\textrm{df}(\lambda) = \textrm{tr}(\boldsymbol{S}) = \sum_{j=1}^p \frac{d_j}{d_j + \lambda}$
임의의 선형회귀모형에 대한 Hat 행렬을 $\boldsymbol{S}$로 나타낸다. 위 식에서는 Ridge에 해당하므로 $\boldsymbol{S} = X(X^TX+\lambda I)^{-1}X^T$으로 정의된다. 이때, $d_j$는 $X^TX$의 고윳값이자 $X$의 특잇값의 제곱근에 해당한다. 단, $j=1$에서 $p$까지 모두 더해주기 때문에 $X$가 Full-rank가 아닌 경우를 고려하면 0 값을 가지는 특잇값도 포함하고 있음을 암시한다. 식을 자세히 들여다보고 의미하는 바를 정리해보자.
○ $\lambda \uparrow$ $\rightarrow$ df($\lambda$)의 분모 $\uparrow$ $\rightarrow$ df($\lambda$) $\downarrow$ $\rightarrow$ 복잡도$\downarrow$
○ $\lambda \downarrow$ $\rightarrow$ rank($X$) $\rightarrow$ 복잡도$\uparrow$
예측 오차 기댓값의 두 번째 항을 자유도와 복잡도의 측도로 볼 수 있는 근거가 위의 내용이다. 예측 오차 이외에도 $\lambda$를 선택하는 데에 사용될 수 있는 모형 선택 기준은 다양하다. 첫 번째로 최소제곱을 최소화하는 관점으로 만들어진 기준들을 소개한다.
○ Mallows’s $C_p = RSS(\lambda)/\sigma^2 + 2\textrm{df}(\lambda)$
○ LOO-CV $= \sum_i \left \{ y_i - \hat{f}_{(-1)}(x_i) = \sum_i (\frac{y_i - \hat{f}(x)_i}{1-S_{ii}})^2 \right \}$, $S_{ii}$는 $\boldsymbol{S}$의 $i$-번째 대각 성분
○ GCV $= \frac{RSS(\lambda)}{(1-\textrm{df}(\lambda)/n)^2}$
세 측도를 구성하는 식들은 예측 오차에서의 두 항과 의미가 거의 같다. 그리고 데이터를 하나씩만 빼가면서 모형을 적합하는 LOO-CV(Leave-one-out cross validation)와 이를 일반화 시킨 GCV(Generalized CV)가 존재하는데, 이들이 갖는 장점은 $\sigma^2$의 추정이 불필요하다는 것이다. 마지막으로 MLE와 MAP를 각각 최대화시키는 아이디어로 만들어진 두 기준 AIC(Akaike information criterion), BIC(Bayesian information criterion)을 소개한다.
○ $\textrm{AIC} = 2L(\hat{\theta}\;|\; X, \boldsymbol{y}) + 2\textrm{df}(\lambda)$
○ $\textrm{BIC} = 2L(\hat{\theta}\;|\; X, \boldsymbol{y}) + log(n)\textrm{df}(\lambda)$
두 기준 모두 작을수록 좋다($L$은 음의 가능도 함수이므로). MAP를 최대화시키는 BIC의 식에 가능도함수만 나타나는 이유는, 모든 모형의 사전분포를 균일 분포로 가정하기 때문이다. 두 번째 항에 공통적으로 $\textrm{df}(\lambda)$가 나타나며, 이는 penalty term임을 말해준다. 즉, 모형 복잡도가 클수록(모수의 수가 많을수록) penalty를 크게 준다는 의미다. $n\geq8$이면 $log(8) > 2$이므로 BIC 기준이 더 큰 penalty를 줌으로써 좀 더 단순한 모형을 선호하게 된다. 여기서 소개한 것들 이외에도 더 많은 모형 선택 기준이 존재하고, 원하는 최적 모형의 목적에 맞게 몇 개의 측도를 골라서 쓰면 된다.
7. 실제 데이터에 대한 Ridge의 적용
OLS와 Ridge를 이용해 대기 오염과 사망률($y$, 10만 명당)의 관계를 추정하여 두 결과를 비교하고, $\lambda$의 중요성에 대해 알아본다. 이 실험에서 고려한 $X$는 대기 오염뿐만 아니라, 잠재적으로 존재할 수 있는 교호 효과의 통제를 위해 기후와 사회경제적(socioeconomic) 변수도 함께 고려한다. 다음은 $X$들을 정리한 표와 $\lambda$에 따른 회귀계수 추정량의 변화 그래프이다.
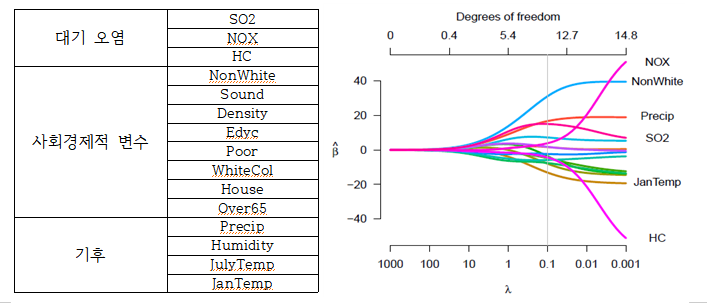
총 15개의 설명 변수를 고려했다. 고차원 자료가 아니긴 하지만, $n=60$으로 매우 작고 $X$들 간에 강한 상관이 존재하여 회귀계수에 대해 ML 추정을 할 경우 문제가 발생하는 자료이다. 이제 오른쪽 그래프를 보자. $\lambda$가 매우 작은 경우, NOX는 사망률에 큰 영향을 미치는데 HC는 오히려 사망률에 대한 강한 보호 효과(Strong protective effect)를 주는 변수처럼 추정이 되었다. HC가 한 단위 증가하면 약 10만 명당 60명의 사람의 생명을 살릴 수 있다는 말이다. 이는 교호 효과로 인해 발생한 직관과 반하는 결과이다. $\lambda$를 증가시킬 경우 NOX와 HC는 0 값을 향해 빠르게 감소한다. 마지막으로 SO2의 계수 값 변화도 언급할 필요가 있다. SO2는 HC와 NOX 각각과 correlation이 존재한다(HC와 NOX 간의 상관만큼 크게 존재하진 않음). 그래서 penalty를 작게준 경우 NOX와 HC의 효과가 나타나게 되고, 그에 따라 증가하는 경향을 띠던 SO2는 오히려 감소하게 된다. 정리하면, SO2의 효과가 HC, NOX 보다 더 중요하게 또는 덜 중요하게 추정되는 것은 $\lambda$의 선택에 달려있다는 뜻이다. 특별히 알아두어야 할 점은 penalty를 증가시킴에 따라 어떤 추정량은 0으로 줄어듦에도 불구하고, 어떤 추정량은 더 유의해지고, 일부는 덜 유의해질 수 있다는 것이다.
앞서 Ridge의 장점에 대해서만 언급했으므로, Ridge가 가지는 한계를 정리하고 글을 마친다.
○ Ridge의 한계는 모든 회귀계수 추정량은 결코 0이 될 수 없다는 점이다. 이는 고차원 회귀에서 두 가지 큰 문제점을 제시한다. 이는 해석의 어려움과 계산비용이 크다는 점이다.
○ 회귀계수 추정량의 축소(Shrinkage)와 변수선택을 동시에 할 수 있는 모형이 필요로 된다. 즉, Ridge의 이점은 유지하면서 동시에 중요한 변수들의 subset을 골라낼 수 있는 모형이 필요하다. 이를 충족시켜주는 것이 Lasso regression이며, 다음에 포스팅할 내용이다.
참고 자료및 사이트
High-Dimensional Data Analysis (Patrick Breheny)
James, Gareth, et al. An Introduction to Statistical Learning. Springer. 2013
"Ridge Regression for Better Usage", Towards data science, last modified Jan 3, 2019, accessed April 8, 2020,
"https://towardsdatascience.com/ridge-regression-for-better-usage-2f19b3a202db"
'고차원 자료분석' 카테고리의 다른 글
| Bias reduction of Lasso estimator (2) | 2020.05.26 |
|---|---|
| Lasso regression (0) | 2020.04.28 |
| 고차원 자료에 대한 고전적인 회귀분석의 문제점 (0) | 2020.04.08 |
| FDR (2) | 2020.04.04 |
| FWER (0) | 2020.04.04 |




댓글