Bias reduction of Lasso estimator

 

❗️블로그 옮김:  https://www.taemobang.com

방태모

※ prerequisite

고차원 데이터에서 고전적인 회귀분석이 가지는 문제점

Ridge regression

Lasso regression

 

 

Lasso regression은 회귀계수 벡터의 $l_1$ norm을 penalty term으로 사용함으로써, 회귀계수의 크기 축소(Shrinkage)뿐만 아니라 변수 선택(Variable selection)의 목적까지 달성할 수 있다. 그러나, 이렇게 추정한 Lasso 추정량(estimator)에는 Bias가 존재한다. 이 글에서는 이러한 Lasso 추정량의 Bias를 줄여줄 수 있는 세 가지 방법론(Adaptive Lasso, SCAD, MCP)에 대해 소개한다.

 

1. Adaptive Lasso regression

 

$Q(\boldsymbol{\beta} | X, \boldsymbol{y}, \boldsymbol{w}) = \frac{1}{2}\left \| \boldsymbol{y} - X\boldsymbol{\beta} \right \|^2 + \lambda \sum_j w_j |\beta_j|$,  where  $w_j = |\tilde{\beta}_j|^{-1}$

 

Adaptive Lasso의 회귀계수 추정량은 위와 같은 목적함수를 통해 구해지며, $\tilde{\boldsymbol{\beta}}$는 초기추정량으로 OLS 또는 Lasso 추정량을 택한다. Adaptive Lasso regression은 초기 추정량이 필요하다는 점을 기억하자. 이 방법론의 아이디어는 큰 계수 추정량일수록 작은 가중치를 줌으로써, bias는 줄이고 sparsity는 유지하는 것이다. 다행히 이러한 효과를 얻는 것에는 아주 정밀한 가중치 $\boldsymbol{w}$의 선택은 요구되지 않는다. 실제, 일치성을 만족하는 초기 추정량(any consistent initial estimator) $\boldsymbol{\beta}$를 통해 $\boldsymbol{w}$에 대한 합리적인 값을 얻을 수 있다. Adaptive Lasso에서 가중치를 설정하는 방식은 다음과 같이 두 가지가 있다.

 

 (1) Two-stage approach

 

$w_j(\tilde{\beta}_j)$

 

 이 접근의 경우 $\lambda$의 변화에는 관계없이($\lambda$에 대해 상수) 가중치는 $\tilde{\beta}_j$에 의해 결정된다. 즉, 앞서 정의한 목적함수는 가중치의 변화가 $\lambda$에 대해서는 상수이므로, Two-stage approach에 해당한다.

 

 (2) Path-wise approach

 

$w_j(\lambda) = w(\tilde{\beta}_j(\lambda))$

 

 "Path-wise approach"에서는 가중치 값이 $\lambda$의 변화에 영향을 받게 된다. 즉, $\lambda$도 재가중(re-weighted) 역할에 참여하게 된다.

 

앞서 정의한 목적함수에서 회귀계수 절댓값의 역수를 반환함으로써 가중치를 갱신하는 함수외에, 어떤 non-increasing 함수 $w(\beta)$라도 초기추정량을 기반으로 가중치를 선택하는 합리적인 방법이 될 수 있다. 다음으로 소개하는 가중치 전략(scheme)은 Two-stage approach 방식으로 적용하는 경우 “Lasso-OLS hybrid”라 부르며, 가중치가 $\tilde{\beta}_j$에 영향을 미치는 Path-wise approach 방식에 적용하는 경우 “relaxed lasso”라고 부른다.

 

$w_j = \left\{\begin{matrix} 0 ,\;\;\; \rm{if} \;\; \tilde{\beta} \neq 0
\\ \infty, \;\; \rm{if} \;\; \tilde{\beta} = 0

\end{matrix}\right.$

 

Lasso-OLS hybrid의 경우, Lasso로 변수 선택을 한 뒤에 OLS로 계수 추정을 수행하는 것과 같다.

 

2. Folded concave penalties(SCAD, MCP)

 

$Q(\boldsymbol{\beta} | X, \boldsymbol{y}, \boldsymbol{w}) = \frac{1}{2}\left \| \boldsymbol{y} - X\boldsymbol{\beta} \right \|^2 + \sum_{j=1}^p P(\beta_j | \lambda, \gamma)$

where $P(\beta_j | \lambda, \gamma)$  is a folded concave penalty

 

concave penalty를 이용해 회귀계수 추정량의 Bias를 줄이는 방법을 소개한다. 이 접근 방법의 경우 $\boldsymbol{\beta}$의 초기추정량은 필요로 되지 않기 때문에 “Single-stage approach”라고도 한다. 위와 같은 목적함수를 통해 회귀계수 추정량이 구해지며, penalty 항으로 concave 함수를 사용한다. 

 

  ○ 모수 $\gamma$의 역할

  $\gamma$는 penalty 항의 concavity를 조절하는 모수로 penalty 함수의 기울기를 얼마나 빠르게 감소시킬지를 결정한다. $\gamma$를 줄일수록 기울기가 빠르게 감소하여 함수를 concave하게 만들기 때문에, Bias뿐만이 아닌 추정량의 안정성(stability)에도 영향을 미친다. 함수가 더 concave 해진다는 말은, local minima(다수의 지역적 최솟값)가 존재할 가능성이 커짐을 말한다. 참고로 “안정성”이란 용어는 목적함수가 하나의 잘 정의된 최솟값으로 안정적이게 최적화된 경우에 쓰인다. 즉, 다수의 지역적 최솟값이 존재하는 함수의 최적화 문제는 매우 불안정(unstable)하다. Bias 측면에서 $\gamma$의 역할을 설명하면, $\gamma$의 크기를 줄일수록 Bias가 작은 추정량을 얻을 수 있고, 반대로 키울수록 Bias가 커지며 결국 $l_1$-penalty로 수렴하게 된다. 정리하면, Folded concave penalties를 사용하는 Lasso regression은 $\gamma$를 줄일수록 목적함수의 concavity가 커져 추정의 안정성은 떨어지지만, Bias가 더 작은 추정량을 얻을 수 있다.

 

많은 non-convex penalties가 존재하는데, 이 글에서는 두 종류의 concave 함수를 소개한다.

 

 (1) SCAD(Smoothly clipped absolute deviations)

 

$P(x|\lambda, \gamma) = \left\{\begin{matrix} \lambda|x|
 & \rm{if}\;\; |x| \leq \lambda, \\ \frac{2\gamma\lambda|x| - x^2 - \lambda^2}{2(\gamma-1)}
 & \rm{if} \;\; \lambda < |x| \leq \gamma\lambda, \\ \frac{\lambda^2(\gamma+1)}{2}
 & \rm{if} \;\; |x| \geq \gamma\lambda
\end{matrix}\right.$     for $\gamma > 2$ 

 

 SCAD의 penalty 함수 $P(x|\lambda, \gamma)$는 위와 같이 주어지며, $x$에 회귀계수 추정량을 대입하면 된다. 보다시피 추정량의 크기가 $\lambda$보다 작은 경우 Lasso와 똑같은 추정을 수행한다. SCAD의 효과는 미분을 통해 좀 더 자세하게 알 수 있다:

 

$\dot{P}(x|\lambda, \gamma) = \left\{\begin{matrix} \lambda
 & \rm{if}\;\; |x| \leq \lambda, \\ \frac{\gamma\lambda-|x|}{\gamma-1}
 & \rm{if} \;\; \lambda < |x| \leq \gamma\lambda, \\ 0
 & \rm{if} \;\; |x| \geq \gamma\lambda
\end{matrix}\right.$

 

즉, SCAD는 추정량의 절댓값이 커질수록 penalty 함수의 기울기를 낮추어 penalty를 연속적으로 완화(relaxed)시키는 역할을 한다.

 

 (2) MCP(Minimax concave penalty)

 

$P_{\gamma}(x; \lambda) = \left\{\begin{matrix} \lambda|x| - \frac{x^2}{2\gamma}
 & \rm{if}\;\; |x| \leq \gamma\lambda,\\ \frac{1}{2}\gamma\lambda^2
 & \rm{if}\;\; |x| > \gamma\lambda
\end{matrix}\right.$     for $\gamma > 1$

 

 MCP의 penalty 함수 $P_{\gamma}(x ; \gamma)$는 위와 같이 주어진다. 미분을 통해 MCP의 효과를 SCAD와 비교하여 알아보자:

 

$\dot{P}_{\gamma}(x; \lambda, \gamma) = \left\{\begin{matrix} \lambda - \frac{|x|}{\gamma}sign(x)
 & \rm{if}\;\; |x| \leq \gamma\lambda,\\ 0
 & \rm{if}\;\; |x| > \gamma\lambda
\end{matrix}\right.$

 

$sign(x)$는 부호 함수로, 음의 실수면 -1, 양의 실수면 1, 0이면 0을 반환해준다. SCAD는 회귀계수의 크기가 일정 값($\lambda$) 이하일 때는 penalty term의 기울기가 $\lambda$로 flat한 형태를 보이지만, MCP는 penalty term의 기울기를 즉시 완화시킨다(relaxed). MCP가 가지는 이러한 특징에서 발생하는 SCAD와의 차이는 다음의 그림에서도 잘 드러난다:

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

 

MCP는 $P(\beta| \lambda, \gamma)$의 기울기를 즉시 감소시켜, Lasso penalty의 path에서 더 빨리 벗어난다. 그에 반면, SCAD는 회귀계수의 크기가 $|\lambda|$ 이하일 때까진 penalty term의 기울기를 감소시키지 않아서 Lasso path와 정확하게 일치한다. 여기서 주목할만한 점은 SCAD가 MCP보다 더 늦은 시점에 penalty term의 기울기를 감소시키지만, 기울기가 0이되는 점은 $|\beta| = \gamma\lambda$로 동일하다는 것이다. 즉, 구간 $(0, \gamma\lambda)$내에서 SCAD는 maximum concavity를 갖게되며, MCP는 기울기를 SCAD보단 좀더 느리게 감소시킴으로써 이 maximum concavity를 최소화(minimize)시킨다. 이러한 이유에서 Minimax concave penlaty라고 부르는 것이다. 이 특징은 다음의 그림에서도 확인할 수 있다.

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

 

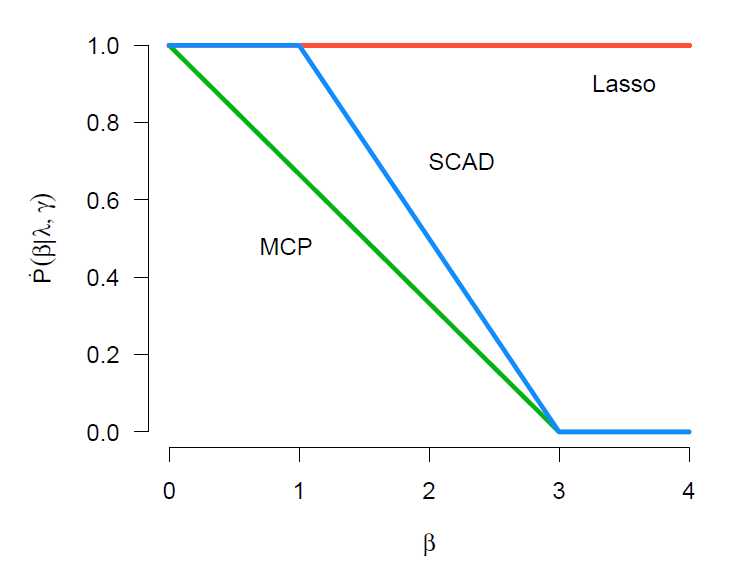
그림을 설명하기 전, 먼저 concavity 측도를 소개한다.

 

$\kappa = \underset{0<t_1<t_2}{sup} \frac{\dot{P}(t_1;\lambda) - \dot{P}(t_2;\lambda)}{t_2 - t_1},$  where sup : 상한(supremum)

 

모든 $t \geq \gamma\lambda$에 대해 $\dot{P}(0+; \lambda) = \lambda$와 $\dot{P}(t; \lambda) = 0$을 만족하는 구간 $(0, \infty)$에서 연속적으로 미분가능한 penalty 함수에 대해, MCP는 maximum concavity를 최소화시킨다. 위 그림에서 SCAD와 MCP의 미분계수는 $\beta = 0$과 $\beta = \gamma\lambda$에서 같은 값을 가진다. 그러나, 이 구간내에서 SCAD는 $\kappa = 1/(\gamma-1) = 1/2$의 maximum concavity를 가지며, MCP는 $\kappa = 1/\gamma = 1/3$의 concavity를 가진다.

 

마지막으로 Lasso, SCAD, MCP 추정량의 path를 OLS 추정량의 변화에 따라 비교한 그래프를 살펴보자. 이 그래프도 각 추정량이 가지는 특성을 직관적으로 이해하는 데에 큰 도움이 된다.

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

 

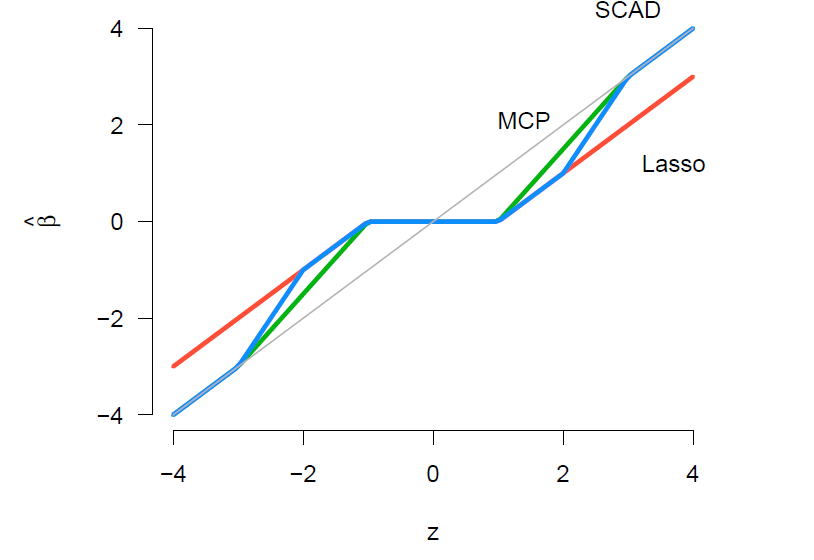
그림의 회색 실선은 정확하게 45도를 이루는 것을 보아 OLS 추정량의 path 나타낸 것임 알 수 있다. 먼저 추정량이 0 근처에 있으면 세 방법론(Lasso, SCAD, MCP) 모두 회귀계수 추정량을 0으로 축소시킨다. 회귀계수의 크기가 일정 값 이상으로 커짐에 따라 MCP는 즉시 penalty 함수의 기울기(변화량)를 감소시켜 점점 OLS의 path로 다가간다. SCAD는 MCP와 달리 penalty 함수의 기울기를 유지시키다가, MCP보다 더 늦은 시점에 기울기를 더 급격하게 감소시켜 더 빠르게 OLS의 path로 다가간다. 그래서 결국, SCAD와 MCP가 OLS path와 일치하게되는 시점은 똑같다. 그에 반면, Lasso 추정량의 경우 회귀계수의 크기에 관계없이 penalty 함수의 기울기를 일정하게 유지시켜, 회귀계수가 커질수록 더 큰 penalty를 부여하여 항상 OLS 추정량보다 더 작은 회귀계수를 가지게 된다.

 

 (3) Firm thresholding과 SCAD thresholding

 

  ○ Firm thresholding

  MCP의 일변량(Univariate) 해(solution)는 Firm thresholding 연산자로 표현할 수 있다.

 

$F(z|\lambda, \gamma) = \left\{\begin{matrix}
\frac{\gamma}{\gamma-1}S(z|\lambda) & \rm{if} \;\; |z| \leq \gamma\lambda, \\ 
z & \rm{if} \;\; |z| > \gamma\lambda
\end{matrix}\right.$,  where $z$ denotes the unpenalized(OLS) solution

 

$\gamma \rightarrow \infty$일수록, Firm thresholding은 Lasso의 일변량 해에 해당하는 Soft thresholding $S(z|\lambda)$로 수렴하며, MCP가 가질 수 있는 $\gamma$의 최솟값인 $\gamma \rightarrow 1$일수록, L0-penalized regression의 해에 해당하는 hard thresholding에 수렴한다. 이처럼 $\gamma$의 변화를 통해 soft thresholding과 hard thresholding간의 gap을 조절하기 때문에 Firm thresholding이라는 이름이 붙은 것이다.

 

  ○ SCAD thresholding

  SCAD의 일변량 해는 SCAD thresholding 연산자로 표현된다. Firm thresholding과 비슷하면서 다소 복잡하다.

 

$T_{SCAD}(z | \lambda, \gamma) = \left\{\begin{matrix}
S(z|\lambda) & \rm{if}\;\; |z|\leq 2\lambda, \\ 
\frac{\gamma-1}{\gamma-2}S(z|\frac{\gamma\lambda}{\gamma-1}) & \rm{if}\;\; 2\lambda < |z|\leq \gamma\lambda, \\ 
z & \rm{if}\;\; |z| > \gamma\lambda
\end{matrix}\right.$

 

이 연산자도 $\gamma \rightarrow \infty$일수록 Soft thresholding 로 수렴하는데, SCAD가 가질 수 있는 $\gamma$의 최솟값인 $\gamma \rightarrow 2$일 때는 hard thresholding으로 수렴하는 것이 아닌 다음의 불연속(discontinuous) 함수로 수렴한다(hard thresholding도 불연속 함수에 해당).

 

$\left\{\begin{matrix}
S(z; \lambda) & \rm{if} \;\; |z| \leq 2\lambda, \\ 
z & \rm{if}\;\; |z| > 2\lambda
\end{matrix}\right.$

 

즉, 두 연산자 $T_{SCAD}$와 $F$ 모두 $\gamma$가 가질 수 있는 최솟값에 근사함에 따라 불연속 함수로 수렴된다.

 

3. Non-convex penalty(SCAD, MCP)를 사용하는 모형의 적합

 

 (1) SNR(Signal to noise ratio) 측도와 $R^2$

 모형 적합에 들어가기 전에 먼저 SNR 측도를 소개한다. SNR을 소개하는 이유는 Simulation Study의 데이터 발생 과정(Data-generating process)에서 쓰이며, 이 측도에 따라 non-convex penalty를 사용하는 회귀계수 추정량에 대한 MSE(Mean squared error)의 path가 달라지기 때문이다.

 

$Var(Y) = Var(E(Y|X)) + E(Var(Y|X)) = \boldsymbol{\beta}^TVar(X)\boldsymbol{\beta} + \sigma^2$

 

선형 회귀에서 $Y$에 대한 분산은 위와 같이 분해되며, 첫 번째 항을 Signal, 두 번째 항을 Noise라고 한다. 이 둘의 비를 “SNR”이라 한다. 이 측도가 데이터 발생에 필요한 이유를 알아보기 위해 먼저 $R^2$를 SNR로 표현해보자:

 

$R^2 = \frac{SSR}{SST} = \frac{Var(E(Y|X))}{\sigma^2 + Var(E(Y|X))} = \frac{Var(E(Y|X))/\sigma^2}{\sigma^2/\sigma^2 + Var(E(Y|X))/\sigma^2} = \frac{SNR}{1+SNR}$

 

만약 simulation design을 하는데, SNR을 50으로 설정했다고 하자. 그럼 이 데이터에 대한 $R^2$는 98%에 달하게 된다. 이렇게 발생시킨 데이터를 현실적이라고 할 수 있을까? 그래서 SNR은 simulation design에서 필수적으로 고려해야 하는 측도이다.

 

 (2) SCAD와 MCP의 회귀계수 추정

 SCAD, MCP의 $\boldsymbol{\beta}$추정에는 좌표 하강법(Coordinate descent algorithm)과 LLA(Local linear approximation) 알고리즘이 쓰인다. LLA 알고리즘을 사용할 경우 추가적인 추정이 요구되어, SCAD와 MCP의 경우에는 좌표 하강법이 더 효율적이다.

 

SCAD와 MCP는 목적함수의 penalty term으로 non-convex penalty를 사용하긴 하지만, 여전히 각 좌표 공간(coordinate dimension)에서는 convex이다(전체 공간에서 convex는 아님). 그래서 local minima(많은 지역적 최솟값)가 존재할 수 있으며, 좌표 하강법과 LLA에서 구해지는 해는 local minima 중 하나에 해당한다. 즉, 좌표 하강법과 LLA 알고리즘은 global minimum으로의 수렴을 보장해주지 못한다.

 

global minimum을 보장을 받기 위해서는 SCAD, MCP 각각에서 다음과 같은 조건이 요구된다.

 

$\left\{\begin{matrix}
\gamma > 1/c_{min} & SCAD, \\ 
\gamma > 1 + 1/c_{min} & MCP
\end{matrix}\right.$

 

$c_{min}$은 $X^TX$의 최소 고윳값(eigenvalue)이며, 위 조건을 만족하는 경우 좌표 하강법과 LLA 알고리즘을 통해 구해지는 해는 목적함수 $Q$의 유일한(unique) global minimum에 해당한다. 항상 이러한 global convexity를 만족시킬 수는 없다. 예를 들어, $p > n$인 고차원 데이터에서는 $X^TX$는 singular matrix로 항상 $c_{min} = 0$에 해당하여 결코 global convexity를 만족할 수 없게 된다. 그래도 한 가지 다행인 점은 $p>n$일 때는 convex penalty를 사용하는 것이 non-convex penalty를 사용하는 경우보다 항상 더 좋은 성능을 내진 않는다는 것이다. 이는 실제로 다음의 그림에서 잘 드러난다.

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

 

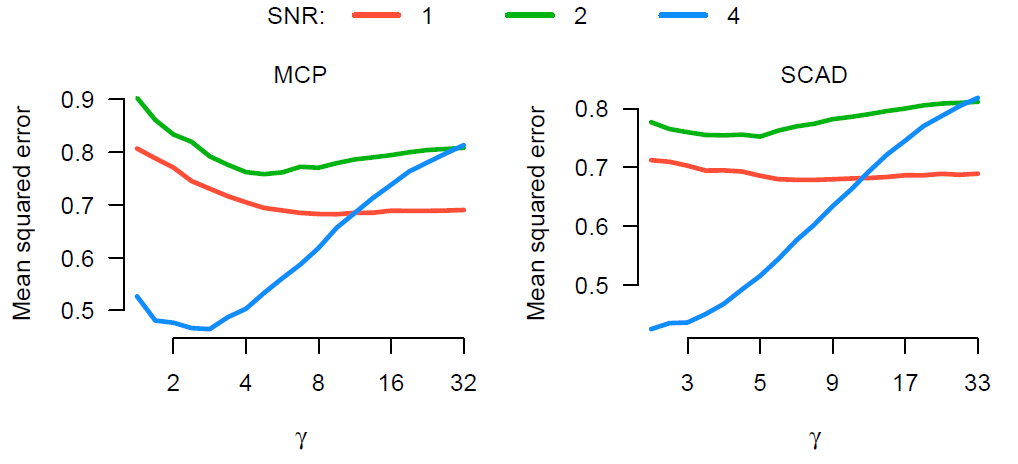
회귀계수 추정량의 MSE에 따른 $\gamma$의 변화를 나타낸 그림이다. SNR 값을 낮게 1 또는 2로 가지는 데이터의 경우, 실제로 $\gamma$를 증가시킴으로써 목적함수를 좀 더 convex로 만들었을 때 오히려 더 나은 계수 추정을 수행하고 있다. 이는 우리의 직관과 일치한다. 이제 SNR 값을 4로 설정하여 생성한 데이터를 보자. 이때는 $\gamma$를 계속해서 증가시켜 목적함수를 convex에 가깝게 만들 경우, 오히려 회귀계수 추정의 정확도가 매우 떨어지는 것을 볼 수 있다.

 

이러한 결과가 발생하는 이유는 SCAD와 MCP를 구해지는 해는 sparse 특성을 가지기 때문이다. 비록 목적함수가 전체 $p$-차원 공간에서 convex(globally convex)는 아닐지도 모르지만, 여전히 그보다 낮은 많은 저차원의 공간에서는 convex이다. 만약 이 저차원 공간 중에 좋은 해(the solution of interest)가 존재한다면, 더 높은 차원의 지역적 최솟값의 존재는 고려하지 않아도 된다. 이러한 개념을 “local convexity”라고 한다.

앞서 배웠던 global convexity의 조건을 떠올려 보자. 이때 조건을 만족시키기 위해 우리가 할 수 있는 간단한 수정은 non-zero인 회귀계수만 $c^*$의 계산에 포함하는 것이다(저차원의 공간만을 고려하자는 뜻과 같다). $\lambda$의 값에 따라서 모형에 포함되는 변수의 집합(the set of active covariates)이 달라지고, 이 집합의 개수는 $\lambda$를 감소시킬수록 증가한다. 즉, 목적함수의 local convexity는 $\lambda$가 클 때는 문제가 되지 않지만, 작을 때는 문제가 될 수도 있다. 이는 다음의 왼쪽 그림에서 잘 드러난다.

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

 

$\lambda = 0.42$과 $\lambda = 0.11$에서는 $\beta_1$, $\beta_2$ 각각이 목적함수를 최소화시킴이 명백하지만, $\lambda = 0.25$의 경우 목적함수의 값들이 매우 flat하여, 둘 중 어느 것이 minimum에 해당하는지 불확실하다. 이러한 상황에는 locally convex 영역을 계산하면 큰 도움이 될 수 있다. 오른쪽 그림에서 빗금이 없는 부분이 locally convex 영역에 해당하고, 이 영역을 통해 실제로 solution path의 어느 영역이 local minima와 불연속(uncontinuous) path로 문제를 일으키는지 알 수 있다.

 

4. 교차 검증(Cross-validation)

 

 (1) Adaptive lasso regression

출처 - High-Dimensional Data Analysis (Patrick Breheny)

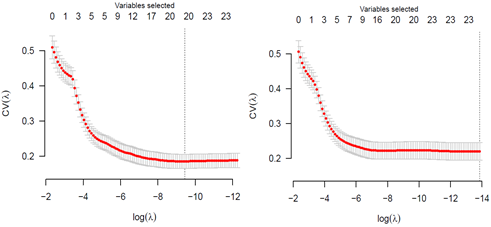
 그림 각각은 Adaptive Lasso 교차 검증이 Biased, Unbiased로 수행된 결과를 나타낸다. Adaptive Lasso의 교차 검증에서는 이렇게 Bias가 발생할 수 있기 때문에 주의 해야할 사항이 있다. 이때 bias가 발생한 이유는 $\boldsymbol{\beta}$의 초기추정량 $\tilde{\boldsymbol{\beta}}$를 얻는 과정에서 이미 left-out fold가 사용되었기 때문이다. left-out fold는 사실상 한 번 쓰인 데이터이며, 그 결과로 예측 오차를 과소 추정하게 되어 bias를 가지게 되는 것이다. 그래서, Adaptive lasso와 같은 two-stage approach에서 예측 오차의 unbiased estimator(비편향 추정량)를 얻기 위해서는, 초기 추정량을 계산하는 과정도 반드시 교차 검증의 과정에 포함해야 한다.

 

 (2) SCAD와 MCP

 SCAD와 MCP는 Adaptive lasso처럼 Lasso 추정량의 bias를 줄이는 결과를 얻어내지만, 초기 추정량이 필요로 되지 않는다. 그래서 교차 검증을 사용하여 예측 정확도의 추론을 수행할 때에는 Adaptive lasso보다 훨씬 더 적합한 접근 방법이 된다. 다음의 교차 검증 결과는 MCP가 실제 데이터 분석에서 추정량의 Bias를 줄이는 것뿐만이 아닌 또 하나의 주요 이점을 보여준다.

 

출처 - High-Dimensional Data Analysis (Patrick Breheny)

왼쪽이 MCP, 오른쪽이 Lasso의 교차 검증 결과이다. MCP가 가지는 또 하나의 이점은 훨씬 더 적은 변수만을 선택하면서 Lasso와 비슷한 예측 성능을 보인다는 것이다(이는 SCAD도 가지는 이점이다). 교차 검증 결과를 보면 실제로 MCP는 27개의 변수만으로, 39개의 변수를 선택한 Lasso와 거의 비슷한 예측 오차를 보여주고 있다.

 

 

참고 자료 
High-Dimensional Data Analysis (Patrick Breheny)