반복측정 분산분석

❗️블로그 옮김:  https://www.taemobang.com

방태모

 

❗ Prerequisite

일원배치 분산분석

❓ More to read
Tutorials on repeated measures design in R

Introduction

반복측정 분산분석(repeated measures ANOVA)은 반복측정 자료에 대한 모평균 비교를 수행하는 분석 방법입니다. 반복측정(repeated measurements)이란, 말 그대로 동일한 실험 단위(experimental unit, EU)에 대해 여러 번의 측정을 하는 경우를 말합니다. 반복측정은 주로 임상시험에서 동일한 환자가 병원을 여러 차례 반복적으로 방문 해 매 방문 때마다 반응치를 측정하는 경우에 일어납니다. 이렇게 얻어지는 반복측정 자료의 주요 목적은 실험군의 평균반응 값이 대조군에서와 동일한지 여부에 있을 것입니다. 이러한 실험 디자인의 비교에 사용되는 분석 방법이 바로 반복측정 분산분석에 해당합니다. 반복측정 분산분석은 반복측정 되는 요인이 하나 일때와 둘 이상인 경우로 나뉩니다. 여기서는 편의상 반복 요인이 1개인 경우에 대해서만 설명하겠습니다. 반복 요인이 2개인 경우는 단순한 확장으로 크게 달라지는 것은 없습니다.

 

1 반복측정 자료의 형태와 모형식

반복측정 자료에서 반복요인은 다양하게 존재합니다. 임상시험에서 동일한 환자가 병원을 여러 차례 반복적으로 방문할 때 마다 반응치를 측정하는 경우에는 반복측정 요인이 "시간(time)"이 되지만, 약의 농도를 증가시켜 한 개체에 대해 반응값을 여러 번 측정하는 경우에는 "약의 농도"가 하나의 반복 요인이 됩니다. 다음의 예제 자료는 반복 요인이 하나인 일반적인 자료 형태에 해당합니다.

 

표 1.1 고혈압 자료

해당 자료는 고혈압 환자 20명을 대상으로 10명에게는 기존의 혈압 강하제(C), 나머지 10명에게는 새로운 혈압 강하제(E)를 투여해 각각 3회에 걸쳐 혈압을 측정하여 정리한 것에 해당합니다. 즉, 첫 방문시 약을 투여 받기 전의 혈압(0주)과 4주 후, 8주 후 혈압을 측정하였습니다. 이 반복측정 자료에 대한 분석 목표는 다음과 같이 3가지로 요약할 수 있습니다.

 

• (1) 기존약과 새로운 혈압 강하제 간 유의한 차이가 있는가?
• (2) 방문 시간에 따라 혈압 차이가 있는가?
• (3) 약과 방문 시간 간에 교호작용이 있는가?

(3) 항목의 반복요인과 처리요인 간의 교호작용의 경우는 분석 전, 자료를 시각화함으로써 가늠할 수 있는 항목에 해당합니다. 예를 들어, 다음은 표 1.1 고혈압 자료를 처리, 방문 시간별 혈압의 평균을 시각화한 그림으로 간략하게 설명을 해보겠습니다.

 

그림 1.1 고혈압 자료

 

그림 1.1을 보면 두 약(혈압강하제 C, E) 간의 효과 차이가 방문 시간(week)에 따라 달라지고 있습니다. 그림이 이렇게 반복 요인에 따라 교차되는 형태를 띨 때 우리는 두 요인 간 교호작용의 존재를 강하게 의심해볼 수 있습니다. 이제 다시 본론으로 돌아가서, 반복측정 자료의 분석 목표 3가지에 따라 반복측정 분산분석에 대한 일반화된 모형식을 작성해보겠습니다. 처리의 수가 $I$개이고, 각 처리에 할당된 개체들을 각각 $n_1, \cdots, n_{I}$(불균형 자료 고려)라고 하고, $i$번째 처리에서 매 $k$ 시점마다 측정한 $j$ 번째 개체의 반응측정치를 $y_{ijk}$라 하겠습니다. 즉, 첨자 $i, j, k$ 각각은 처리, 개체, 시간을 나타냅니다. 이에 따른 반복측정 분산분석의 모형식은 다음과 같이 주어집니다:

 

\begin{equation} y_{ijk} = \mu + \alpha_i + \beta_{ij} + \gamma_{k} + \delta_{ik} + \epsilon_{ijk} \\ (i = 1, \cdots, I; \ j = 1, \cdots, n_i; \ k = 1, \cdots, K) \end{equation}

 

여기서 $\mu$는 반응측정치 $y_{ijk}$의 전체평균을 나타내는 모수, $\alpha_i$는 $i$번째 처리 효과(treatment effect), $\beta_{ij}$는 $i$번째 처리 내에서의 개체 $j$의 효과(subject effect), $\gamma_k$는 시간 $k$의 효과, $\delta_{ik}$는 처리 $i$와 $k$번째 시간의 교호작용효과(interaction effect)이며 오차항 $\epsilon_{ij} = (\epsilon_{ij1}, \cdots, \epsilon_{ijK})^`$는 평균이 $0$인 독립적인 정규분포를 따른다고 가정합니다. 표 1을 식 (1)로 표현한다면, $I$는 2, $n_{1} = n_{2} = 10$, $K = 3$이 될 것입니다. 식 (1)의 일반화된 모형식을 따라 반복요인이 하나인 반복측정 자료의 형태를 나타내보면 다음과 같습니다:

 

표 1.2 반복요인이 하나인 반복측정 자료의 형태

 

2 구형성 가정

반복측정 분산분석이 다른 분산분석과 구분되는 특징적인 부분은 오차항에 대한 추가적인 가정이 이루어진다는 것입니다. 그것은 바로 오차항의 공분산 행렬에 대해 복합대칭성(compound symmetry) 또는 구형성(sphericity)을 가정하는 것입니다. 엄밀히 말하면 복합대칭성은 구형성의 특수한 경우인데, 여기서는 이 둘을 같은 것으로 보고 설명하려고 합니다.^[각주:1] 복합대칭성 가정이 필요한 이유는 반복측정에서 개체들은 일정한 시점마다 측정되기 때문에 각 반복측정치들 간에 어느 정도 상관관계가 존재하기 때문입니다. 복합대칭성이란 이러한 반복요인의 처리간 상관관계가 모두 동일하다는 것으로, $K$개의 시점에 대한 오차항이 복합대칭성을 만족할 때 공분산 행렬의 형태는 다음 식과 같이 주어집니다:

 

\begin{equation} {\rm{COV}}(\epsilon)_{K \times K} = \sigma^2 \begin{bmatrix}1 & \rho & \cdots & \rho \\ \rho & 1 & \cdots & \rho \\ \vdots &  & & \vdots  \\ \rho & \cdots & \rho & 1   \end{bmatrix} \end{equation}

 

즉, 모든 측정 시간($k = 1, \cdots, K$)에서의 분산은 $\sigma^2$으로 같고 공분산도 모든 시간에 대해 $\sigma^2 \rho$로 같다고 가정합니다. 이러한 복합대칭성은 반복측정 자료를 일변량(univariate)으로 분석하기 위한 조건이 됩니다. 실제 자료에서 이러한 오차항의 복합대칭성 또는 구형성을 만족하기는 쉽지 않습니다. 특히 시간의 간격이 일정하지 않은 경우 이러한 가정이 깨지는 예가 많습니다. 그래서, 반복측정을 하는 형태의 RCT를 수행할 계획이 있는 연구자분들은 이점을 꼭 유념하셔서, 측정 시점이 중요하게 정해져 있는 실험이 아니라면 등간격으로 반복측정 계획을 세우시는 것을 권장합니다. 만약, 자료의 구형성 가정이 깨졌을 경우는 반복측정 분산분석을 통한 일변량 분석을 그대로 적용하는 것은 잘못된 결과를 유도할 수 있습니다. 이를 피할 수 있는 방법은 다변량 분산분석을 이용한 접근법인데 이는 <4 다변량 접근법>에서 서술하겠습니다.

 

오차항의 구형성 가정 만족 여부는 처리들을 대비(contrast) 또는 직교다항(orthogonal polynomials)을 만족하도록 변환시킨 후 대비행렬 또는 직교다항행렬의 오차항에 대한 검정을 통해 체크할 수 있습니다.^[각주:2] 만약 구형성 조건이 만족되지 않을 경우에는 다변량 분산분석의 결과를 사용하는 것이 좋습니다. 그러나, 만약 구형성 조건이 만족되는 경우에는 반복측정 분산분석 모형을 사용하는 것이 검정력(power)^[각주:3]을 더 높일 수 있습니다. 구형성 조건이 만족되는 경우에는 다변량 방법을 썼을 때는 지나치게 보수적인 검정을 수행하게 된다고 알려져 있습니다. 그리고, 구형성이 깨진 경우에도 이를 보정한 후 반복측정 분산분석을 이용해 일변량 분석을 수행할 수도 있습니다. 반복측정의 분산과 공분산의 함수인 Greenhous-Geisser Epsilon($\epsilon$)이라는 보정항을 계산할 수 있는데, 이 보정은 분산분석에서의 자유도에 $\epsilon$을 곱하여 수정된(adjusted) 자유도를 제공합니다. 그 외 Huynh-Feldt Epsilon 값을 이용한 보정방법을 쓰기도 합니다. 이 값들이 모두 1근처의 값을 갖고 있으면 구형성 조건을 만족한다고 볼 수 있습니다. 그러나, 구형성 검정이 매우 유의한 경우(p-value가 매우 작은 경우)에는 일변량 분석에서 보정을 수행한다고 하여도, 다변량 분산분석에 의한 결과가 달라질 수 있고 이 때에는 다변량 접근법을 이용하는 것이 좋다고 할 수 있습니다.

 

3 연구 가설과 분산분석 표

표 1.1과 같이 처리의 수가 하나가 아닌 여러 개가 존재하면 처리의 효과와 함께 시간과 처리의 교호작용 효과에 대한 검정이 연구 가설에 추가됩니다. 즉, 3개의 연구가설을 세워 검정을 수행할 수 있습니다:

 

  - $H_{01} = \alpha_1 = \alpha_2 = \cdots = \alpha_{I} = 0$ (처리 간의 반응치에 차이 없음)

  - $H_{02} = \gamma_1 = \gamma_2 = \cdots = \gamma_K = 0$ (시간 간의 반응치에 차이 없음)

  - $H_{03} = \delta_{11} = \delta_{12} = \cdots = \delta_{IK} = 0$ (처리와 시간 간의 교호작용 존재 하지 않음)

 

이 3가지 가설의 검정을 위한 변동의 분해는 다음과 같이 이루어집니다:

 

\begin{equation} SST = SSI + SSJ + SSK + SS_{I \times K} + SSE \end{equation}

 

구형성을 만족하는 경우 일변량 분석에 대한 분산분석 표는 다음과 같습니다. 여기서 $N = \sum_{i=1}^I n_i$에 해당합니다.

 

요인	자유도	제곱합	평균제곱합(MS)	F
처리	$I-1$	$SSI$	$SSI/(I-1)$	$\rm{F}_1$
개체(처리)	$N-I$	$SSJ$	$SSJ/(N-I)$
시간	$K-I$	$SSK$	$SSK/(K-1)$	$\rm{F}_2$
처리 $\times$ 시간	$(I-1)(K-1)$	$SS_{I \times K}$	$SS_{I \times K}/(I-1)(K-1)$	$\rm{F}_3$
오차	$(N-I)(K-1)$	$SSE$	$SSE/(N-I)(K-1)$
계	$NK-1$	$SST$

 

다음은 제곱합의 식들을 정리한 것입니다:

 

 - $SSI = K \sum_{i=1}^I n_i ({\bar{y}}_{i\cdot \cdot} - {\bar{y}}_{\cdot \cdot \cdot})^2$

 - $SSJ = K \sum_{i=1}^I \sum_{j=1}^{n_i} ({\bar{y}}_{i j \cdot} - {\bar{y}}_{i\cdot \cdot})^2$

 - $SSK = N \sum_{k=1}^{K} ({\bar{y}}_{\cdot \cdot k } - {\bar{y}}_{ \cdot \cdot \cdot})^2$

 - $SS_{I \times K} = \sum_{k=1}^K \sum_{i=1}^I n_i({\bar{y}}_{i\cdot k} - {\bar{y}}_{i\cdot \cdot} - {\bar{y}}_{\cdot \cdot k} + {\bar{y}}_{\cdot \cdot \cdot})^2$

 - $SSE = \sum_{k=1}^K \sum_{i=1}^I \sum_{j=1}^{n_i} (y_{ijk} - {\bar{y}}_{i j \cdot} - {\bar{y}}_{i\cdot k} + {\bar{y}}_{i\cdot \cdot})^2$

 - $SST = \sum_{k=1}^K \sum_{i=1}^I \sum_{j=1}^{n_i} (y_{ijk} - {\bar{y}}_{ \cdot \cdot \cdot})^2$

 

여기서 주의할 것은 처리에 대한 $\rm{F}$-값은 처리에 대한 평균제곱합($\rm{MSI}$)을 처리 내 개체의 평균제곱합($\rm{MSJ}$)로 나눈다는 것이다. 따라서 처리내 개체의 효과는 하나의 오차제곱합으로 볼 수 있다. 결론적으로, 각 가설을 검정하기 위한 $\rm{F}$ 값 $\rm{F}_1$, $\rm{F}_2$, $\rm{F}_3$을 정리하면 다음과 같다. 

 

  - ${\rm{F}}_1 = \frac{SSI/(I-1)}{SSJ/(N-I)} \ \sim \ F(I-1, N-I)$

  - ${\rm{F}}_2 = \frac{SSK/(K-1)}{SSE/(N-I)(K-1)} \ \sim \ F(K-1, (N-1)(K-1))$

  - ${\rm{F}}_3 = \frac{SS_{I \times K}/(I-1)(K-1)}{SSE/(N-I)(K-1)} \ \sim \ F((I-1)(K-1), (N-I)(K-1))$

 

4 다변량 접근법

다변량 접근법이란, 말그대로 반복측정 자료를 다변량 자료로 간주하고 접근하여 다변량 분산분석(multivariate ANOVA)을 통해 분석을 진행하는 방식을 말합니다. 즉, 반복된 측정치들을 다변량 반응벡터로 취급하여 종속변수들의 상관관계를 인정한채로 분석을 진행하기 때문에, 일변량 분석보다 구형성 가정에 대해 로버스트(robust) 하다고 할 수 있습니다. 예를 들어 표 1.1 고혈압 자료의 경우, 각 집단의 다변량 반응벡터는 (0주 혈압 측정치, 4주후 혈압 측정치, 8주후 혈압 측정치)$^`$가 되는 것입니다.

 

다변량 분석의 결과는 반복요인에 대해 Wilk's Lambda, Pillai's Trace, Hotelling-Lawley, Roy's Greatest Root의 4가지 검정통계량을 제시해주며, 각 검정통계량의 p-value가 작을수록 귀무가설을 기각시킬 수 있는 가능성이 커집니다. 그리고, 처리 요인의 경우에는 반복측정 분산분석을 통한 일변량 분석의 처리요인에 대한 검정 결과와 동일한데, 이는 다변량 분산분석이 반복요인에 대한 오차항의 구형성 조건이 만족되지 않을 때 실시하는 분석방법이기 때문에, 반복요인이 아닌 처리에 대해서는 오차항의 구형성 조건을 검정할 필요가 없고 따라서 굳이 다변량 분석을 수행하지 않아도 되기 때문입니다.

 

5 RCBD와의 관계

사실 반복측정 분산분석이 RCBD(randomized complete block design, 랜덤화 완전 블록 설계)와 직접적인 관계가 있는 것은 아닙니다. 그럼에도 불구하고 RCBD와의 관계를 짚고 넘어가려는 이유는, 표 1.1과 같은 시점에 따른 반복측정과 처리요인이 존재하는 자료 형태가 아닌, 간혹 존재하는 측정 시점 자체 하나만을 요인으로 간주하는 반복측정 자료와 그에 따른 모형식이 RCBD의 자료 형태 및 모형식과 상당히 유사하기 때문입니다. 예를 들어, 측정 시점만을 하나의 요인으로 간주하는 반복측정 자료의 예는 다음과 같습니다:

 

표 3.1 측정 시점을 요인으로 하는 반복측정 자료

 

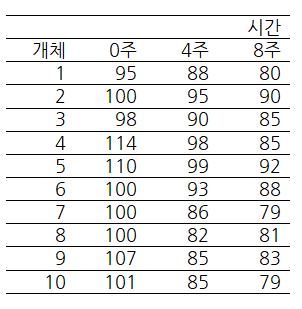
해당 자료는 한 운동 프로그램의 체중 감량 효과를 측정하기 위해 개인의 체중을 3개의 시점(0주, 4주, 8주)에서 측정한 결과입니다. 0주는 운동 시작 전 몸무게, 4주, 8주는 각각 운동프로그램을 주 5회 수행하기 시작한 뒤의 4주 후, 8주 후 몸무게에 해당합니다. 이 반복측정 자료의 분석 목표는 "몸무게 측정 시점에 따라 몸무게 차이가 있는 가?"입니다. 즉, 운동 프로그램의 체중 감량 효과를 보는 것이죠. 이러한 디자인은 관심요인과 블록요인이 각각 하나인 RCBD와 상당히 유사합니다. 관심요인은 체중, 블록요인은 개체(사람)으로 볼 수 있겠죠.^[각주:4] 모형식을 써봐도 상당히 유사합니다. 먼저, 식 (1)의 형태로 따라 써보면 다음과 같습니다:

 

\begin{equation} y_{ij} = \mu + \beta_j + \gamma_{k} + \epsilon_{ij} \\ j = 1, \cdots, 10; \ k = 1, 2, 3   \end{equation}

 

표 3.1을 RCBD라고 생각하고 모형식을 써보면 다음과 같습니다:

 

\begin{equation} y_{ij} = \mu + \beta_i + \tau_j + \epsilon_{ij} \\ i = 1, \cdots, 10; \ j = 1, 2, 10   \end{equation}

 

여기서 $\beta$는 $i$번째 블록효과, $\tau$는 $j$번째 수준의 처리효과에 해당합니다. 식 (3)과 (4)는 표현 문자만 다를 뿐, 모형식 자체는 정확하게 일치합니다. 예를 들어, 표 3.1 자료가 R을 이용하여 반복측정 분산분석과 RCBD를 수행하면, 둘의 분산분석표는 정확하게 같을겁니다. 그러나, 둘 간의 가장 큰 차이점은 진행되는 분석에서 내포되어 있는 가정에서 발생합니다. 반복측정 분산분석의 경우 반복측정된 자료의 특성을 반영하여 처리 그룹간에 어느정도의 상관(correlation)이 존재하는 것을 반영하여 오차항에 구형성 가정을 하며, 반대로 RCBD의 경우 처리 그룹간 독립을 가정하여 오차항을 평균이 0이고 분산이 $I \sigma^2$인 정규분포를 따른다고 가정합니다. 사실 실제 표 3.1과 같은 자료를 다루는 상황에서, 분석자가 반복측정 분산분석을 사용할 지, RCBD를 사용할 지 고민하는 일은 없을 거라 생각됩니다. 측정 시점 그 자체가 하나의 요인이라면 반복측정 자료임은 자명하기 때문이죠. 그저 혼자 공부를 하며 반복측정 자료의 여러 형태들을 들여다보다가, 표 3.1과 같은 형태는 그 형태가 반복측정이라는 것을 제외하면 RCBD의 자료 구조와 상당히 유사하여 그 근본적인 차이를 알아보기 위해 여기까지 오게 됐습니다.😂 이 글을 읽으시는 분들은 그러한 조금의 혼동도 없길 바라는 마음입니다.😃

 

Summary

이번 글에서는 반복측정 분산분석을 주제로 하여, 반복측정 자료에 대한 전반적인 분석 방법에 대해 알아보았습니다. 마지막으로 반복측정 자료에 대한 분석 과정을 간략하게 요약하고 글을 마치겠습니다.

 

  i) 결측치 사전 제거 및 반응치(반응변수)에 대한 정규성 가정 검토^[각주:5] 

  ii) 구형성 가정 검토

  iii) 분석 수행

    - 구형성 가정 만족: 반복측정 분산분석을 이용한 일변량 분석 수행

    - 구형성 가정이 크게 벗어나지 않음: Greenhouse-Geisser 등의 방법을 이용한 수정된 일변량 분석 수행

    - 구형성 가정 만족X: 다변량 분산분석 수행

  iiii)

    - 구형성 가정이 만족될 경우, 단변량 분석을 수행하면 처리 효과의 차이를 감지해내는 능력인 검정력이 떨어짐

   - 다변량 분석은 공분산 행렬에 아무런 가정없이 가능하지만, 개체의 수가 적은 경우 검정력이 매우 떨어짐. 따라서, 구형성 가정이 만족이 안되더라도 아주 크게 벗어나지 않는다면 어느정도의 수정을 거쳐 일변량 분석을 수행하는 것이 좋은 방안임(Greenhouse-Geisser, Huynh-Feldt 방법 등)

 

 

📝 참고 문헌

[1] 이재원, 박미라, 유한나. (2006). 생명과학연구를 위한 통계적 방법. 자유아카데미

[2] 나종화. (2017). R 응용 다변량분석. 자유아카데미

[3] statistics.laerd.com/statistical-guides/repeated-measures-anova-statistical-guide.php

---

1. 좀 더 디테일하게 말하면, 반복 처리요인간 상관이 동일함을 의미하는 복합 대칭성과 각 처리마다 처리 내 분산들이 동일함을 의미하는 등분산(equal variance)이 모두 만족되는지 보기 위해 구형성 검사(Mauchly's test)를 수행함 [본문으로]
2. 구형성 검정(sphericity tests)은 Mauchly's Criterion이라 불리는 카이제곱 검정에 기초함 [본문으로]
3. 최대한 간략히 설명하면 귀무가설을 기각시킬  가능성이라 할 수 있음 [본문으로]
4. 사람에 따라서 운동 프로그램의 효과가 다를 수 있기 때문에 [본문으로]
5. 실험설계의 기본원리(랜덤화, 반복, 블록화)가 잘 지켜진 실험이라면 정규성 검토 불필요 [본문으로]