검정력과 검정력 함수에 대해

❗️블로그 옮김:  https://www.taemobang.com

방태모

※ prerequisite

통계적 가설검정의 원리

 

앞으로의 설명은 편의상 평균이 $\mu$이고, 분산이 $\sigma^2$인 정규모집단으로 부터의 확률표본(random sample)에 기초한 모평균($\mu$)에 대한 우단측 검정을 기준으로 한다. 본격적인 내용에 들어가기 전에 1종 오류와 2종 오류에 대해 알고가자.

 

• 1종 오류(Type I error) : 귀무가설이 참인데, 이를 기각시키는 오류
• 2종 오류(Type II error) : 귀무가설이 참이 아닌데, 이를 기각시키지 못하는 오류

 

출처 - https://www.abtasty.com/blog/type-1-and-type-2-errors/

 

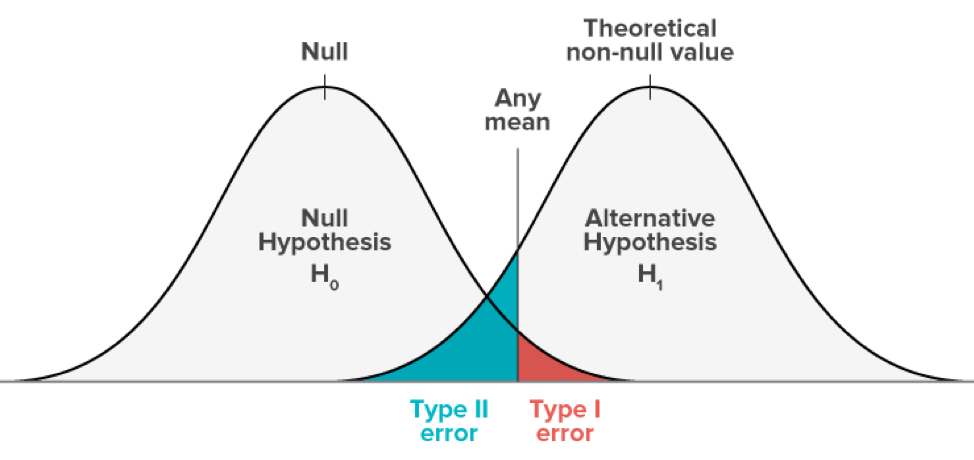
모평균에 대한 검정이므로 표본평균을 검정통계량으로 쓴다. 즉 위 그림의 Any mean은 검정통계량 관측값을 말한다. 그림을 보면 알 수 있듯, 우리는 1종 오류와 2종 오류를 동시에 통제할 수 없다. 그래서 우리는 더 심각한 오류라고 생각되어지는 1종 오류를 컨트롤 한다. 1종 오류가 더 심각한 오류인 이유라고 하는 이유는 뭘까? 예를 들어, 신약 개발을 위해 기존약과 약효를 비교 해야하는 상황을 생각해보자. 이때,  실제로는 기존약의 효과가 더 우수한데, 신약의 효과가 더 좋다고 판단하는 1종 오류를 범했다. 그럼 제약회사는 신약 대량 생산을 위한 준비로 큰 비용을 소모할 것이다. 이와 같이 1종 오류는 잘못된 의사결정에 큰 비용까지 초래하므로, 이러한 관점에서 더 안좋은 오류라고 한다. 앞서 말한 예의 상황은 생산자의 입장이다. 그래서 품질관리 분야에서는 1종 오류를 "생산자 오류"라고도 한다.

 

1. 검정력 함수(Power function)

검정력 함수는 "귀무가설을 기각시킬 확률"을 모수 값의 함수로 나타낸 것이다. 잠깐 외람된 말을 하면 어떤 검정법을 소개하는 것에 있어서, "검정력(Power)이 강하다." 라는 것은 귀무가설을 다른 검정에 비해 비교적 잘 기각시키는 특징을 가짐을 말하며, liberal 또는 optimistic으로 표현하기도 한다. 반대로 "검정력이 약하다." 라는 것은 귀무가설을 다른 검정에 비해 비교적 잘 기각시키지 못하는 특징을 가짐을 말하며, conservative(보수적인)라고 표현한다. 이런 표현을 알아두면 검정법에 대해 공부할 때 편할것이다. 이제 원래 얘기로 돌아가자. 검정력 함수에서 고려하는 임의의 모수를 $\theta$라 했을 때, 다음과 같이 쓸 수 있다.

 

$\gamma = P_{\theta}(\textrm{reject}\; H_0\;|\; \theta) = P_{\theta}(\bar{X}>c)$

 

유의수준을 이용한 검정법을 생각했을때, 검정통계량이 기준값 $c$보다 크면 귀무가설을 기각할 수 있으므로 위와 같이 정의할 수 있다. 여기서 $\theta$는 귀무가설이 참인 영역에 포함될 수도 있고, 대립가설이 참인 영역에 포함될 수도 있다.

 

검정력 함수

 

모수값(여기선, 모평균 검정이므로 $\mu$)의 변화에 따른 검정력 함수의 그림을 나타낸 것이다. 이 그림만 해석하면 다 끝난다. 천천히 그림을 해석해보자.

 

먼저 그림의 $\theta_{0}$는 가설을 떠올리면 된다. 모평균 $\mu$에 대한 우단측 검정을 가정한다고 했으므로 $H_{0} : \theta \leq \theta_{0}$에서의 $\theta_0$를 의미한다. 당연히 이를 기준으로 귀무가설이 참인 영역, 대립가설이 참인 영역으로 구분된다. 그에따라 $\alpha_{\theta}$, $(1-\beta_{\theta})$로 검정력 함수를 나타낼 수 있다. 귀무가설이 참인 영역에서의 검정력 함수를 $\alpha_{\theta}$라 나타낸 이유는 검정력 함수는 "귀무가설을 기각시킬 확률"을 나타낸것이므로, 귀무가설이 참인 영역에서의 기각시키는 행위는 1종 오류되기 때문이다(보통 1종 오류를 $\alpha$라 나타냄). 이때 $\alpha_{\theta}$의 최댓값은 점 $\theta_0$에서 주어지며, 이를 유의수준(significance level)이라 부른다. 통계적 가설검정의 원리에서 유의수준을 이용한 검정방법 생각하면, "유의수준은 분석자가 알아서 정하는거라고 알고있는데?" 이게 뭔말이지? 할 수 있는데, 유의수준의 수리통계학적 정의라고 편하게 생각하면 될 것 같다. 이따가 마지막에 수식으로 정의할 것이며, 이렇게 수식으로 정의할 수 있는 유의수준을 통해 "어떤 검정이다." 라고 일컫는다. 이 글의 마지막에 뭐라고 표현하는지 알 수 있다. 그러니까 헷갈리지말라는 얘기다. 대립가설이 참인 영역에서는, 귀무가설을 기각시키는 행위는 올바른 짓이다. 그래서 이 영역에서는 검정력 함수를 $(1-\beta_{\theta})$라고 정의할 수 있다. 그럼 마지막으로 검정력 함수가 위와 같이 0-1 범위에서 곡선형태를 띄는 이유에 대해 생각을 해보자. 귀무가설에서 설정되는 $\theta_0$는 귀무가설이 참인, 거짓인 영역을 결정짓는 이론적인 기준이다. 이 값의 추정에는 관측자료들이 필요하고, 모평균 검정에서는 이 관측자료들의 평균을 통해 $\theta$를 추정한다. 이 추정값이 커질수록 귀무가설의 중심위치(평균)인 $\theta_0$로부터 멀어지게 되고, 귀무가설을 기각시킬 확률이 1에 가까워진다. 반대로, 작을수록 귀무가설의 중심위치로부터 가까워지며 극단적으로는 더 작은 값이 나올수도 있다. 그럼 이 경우 귀무가설을 기각시킬 확률은 0에 가까워진다. 이러한 이유에서 검정력함수는 0-1 범위에서 움직이는 것이다.

 

이제 앞서 말한것들을 수리통계학적인 수식을 통해 정의하자. 위 내용을 이해했으면, 수식정의는 어렵지 않다. 먼저 확률표본과 가설을 정의하고, 이에 대한 검정을 수행할 것이라고 하자.

 

$X_1, \cdots, X_n \; \widetilde{iid} \; f(x; \theta)$

$H_0 : \theta \in \Omega_0\;\; vs \;\; H_1 : \theta \in \Omega_1\;,\; \Omega_0 \cup \Omega_1 = \Omega $ (전체 모수 공간)

 

먼저 확률표본들의 공간을 겹치는 곳이 없도록 분할한다. $A = \left \{(x_1, x_2, \cdots, x_n)\;|\; f(x_1, x_2, \cdots, x_n) > 0 \right \}$ 이라하고 $A$를 $C$와 $C^{\ast}$로 분할한다. 즉, $A = C \cup C^{\ast}$ (단, $C \cap C^{\ast} = \phi $)

 

1. 기각역(Critical region)

$(X_1, \cdots, X_n) \in C$이면 귀무가설을 기각하고, $(X_1, \cdots, X_n) \notin C$이면 귀무가설을 기각하지 못함을 결정하는 영역 $C$를 기각역이라고 한다. 즉 다음을 만족하는 영역 $C$를 기각역으로 정의한다.

 

$(X_1, \cdots, X_n) \in C \Leftrightarrow  \textrm{reject}\; H_0$ 

 

2. 검정(또는 검정함수) (test or test function)

기각역이 $C$인 검정(또는 검정함수) $\phi$로 나타낸다고 했을 때, 검정력함수(Power function)는 $\gamma_{\phi}(\theta) = P_{\theta}(X \in C) = E_{\theta}\left[ \phi(X_1, \cdots, X_n) \right]$로 정의된다. 즉, 검정함수에 기댓값을 씌운 것이 검정력 함수다. 또한, 한점 $\theta_1 \in \Omega_1$에서의 검정력 함수 값 $\gamma_{\phi} = P_{\theta_1}(X \in C)$을 그 점에서의 검정력(Power)라고 한다. 다시 말하면! 검정력은 대립가설이 참인 영역에서, 귀무가설을 기각시킬 확률이다.

 

3. 제 1종 오류, 제 2종 오류

(1) 제 1종 오류(Type I error)

검정 $\phi$에 대한 1종 오류를 정의한다.

 

$\gamma_{\phi}(\theta) = P_{\theta}(X \in C)\;, \theta \in \Omega_0 = \alpha(\theta)$

 

즉, 귀무가설이 참인 영역에서 귀무가설을 기각시킬 확률

 

(2) 제 2종 오류(Type II error)

검정 $\phi$에 대한 2종 오류를 정의한다.

 

$1-\gamma_{\phi}(\theta) = 1-P_{\theta}(X \in C), \theta \in \Omega_1 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = 1 - (1-\beta(\theta)) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;= \beta(\theta)$

 

즉, 대립가설이 참인 영역에서 귀무가설을 기각하지 못할 확률을 의미한다.

 

여기서 제 1종 오류는 귀무가설이 참인 영역에서의 검정력(검정력함수의 함수값)을 의미하는 것으로 흔히 $\alpha_{\phi}(\theta)$ 로 나타내며, 제 2종오류는 $\beta_{\phi}(\theta)$로 나타낸다. 이를 바탕으로 모수의 영역에 따라 검정력 함수를 정의하면:

$\gamma(\theta)\left\{\begin{matrix} \alpha(\theta)\;, \; \theta \in \Omega_0
\\ 1-\beta(\theta)\;,\; \theta \in \Omega_1

\end{matrix}\right.$

 

4. 유의수준(Significance level)

귀무가설 영역이 참인 영역에서 검정력 함수의 최댓값(우단측 검정 기준)이 유의수준에 해당한다. 이를 수식으로 나타내면:

 

$\alpha = \underset{\theta \in \Omega_0}{super} \, \alpha_{\phi}(\theta) \;\; \textrm{or}\;\; \underset{\theta \in \Omega_0}{super} \, \gamma_{\phi}(\theta)$

 

이를 "검정 $\phi$의 유의수준", 또는 "기각역 C의 크기(Size)"라 한다. 여기서 말하는 유의수준 또는 검정역의 크기는 귀무가설의 $\theta_0$를 어떻게 설정하느냐에 따라 달라질 것이다. 우단측 검정 기준에서, $\theta_0$를 크게 잡을수록 엄격한 검정을 수행하는 것이다(엄격하다는 표현은 귀무가설을 기각시키기 어려움을 나타낸다).  또한, 제 1종 오류의 최댓값 즉, 크기(Size)가 $\alpha$ 이하인 검정(또는 기각역)을 수준(level)이 $\alpha$인 검정(또는 기각역)이라 부르기도 한다. 

 

 

참고한 책

나종화 (2012). 수리통계학. 자유아카데미