❗️블로그 옮김: https://www.taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 통계학을 전공으로 학부, 석사를 졸업했습니다. 현재는 가천대 길병원 G-ABC에서 Data Science를 하고있습니다. 통계학, 시계열, 통계적학습과 기계
www.taemobang.com
"확률변수(random variable : r.v.)는 분포를 가진다"
확률변수라는 것이 정의될 때뿐만 아니라 수리통계학에서 위 개념을 가지고 접근하는 것이 매우 중요하다.
1. 확률변수(random variable : $r.v.$)
확률변수 $X$는 표본 공간에서 정의되는 실숫값을 취하는 함수(real-valued function)이다.
$ X : S \rightarrow R $
여기서 $S$는 표본 공간(Sample space)를 의미하며, R은 실수 영역를 의미한다. 이해를 돕기위해 예를 들어보자. 공정한 주사위를 1회 던지는 확률실험에서 표본공간은
$S$ = $\left\{1, 2, 3, 4, 5, 6\right\}$ $\equiv$ $\left\{w_1, w_2, \cdots, w_6\right\}$
으로 정의되며, 표본공간에서 정의되는 함수 $X$를 $X\left(w\right)$ = 원소 $w$의 짝수의 수, $w\in S$ 와 같이 정의하면, 함수 $X$는 실수값을 가지는 함수이므로 확률변수가 된다. 이때, $X$의 영역(range)는 $A$ = {0, 1}이 된다.
후의 포스팅에서 다루게될 이산형 확률분포와 연속형 확률분포에 대해서 주의해야 할 점 하나를 먼저 언급하자면, 혈액형이나 성별과 같은 이산형(discrete) 확률분포에서의 한 점에서 함숫값(막대의 높이)은 그 점의 확률을 의미하지만, 키나 몸무게와 같은 연속형(continuous) 확률분포에서의 함숫값은 그 자체로 확률을 의미하는 것이 아니라는 것이다. 연속형 분포에서 함수값은 곧 그 값 주변의 값을 취할 가능성을 상대적 높이로 나타낸 것이라 할 수있다. 따라서 연속형 분포의 확률밀도함수의 $f(x)$의 경우 아랫부분의 면적이 1을 만족할 뿐이며, 한 점에서 함숫값 자체는 얼마든지 1보다도 클 수 있다. 단적인 예로 연속형 확률분포 중 하나인 지수분포를 떠올려보자. 해당 분포의 모수 $\lambda$에 따른 지수분포의 형태는 다음과 같이 주어지며, 보이는 바와 같이 함숫값이 1이 넘는 경우도 존재한다:
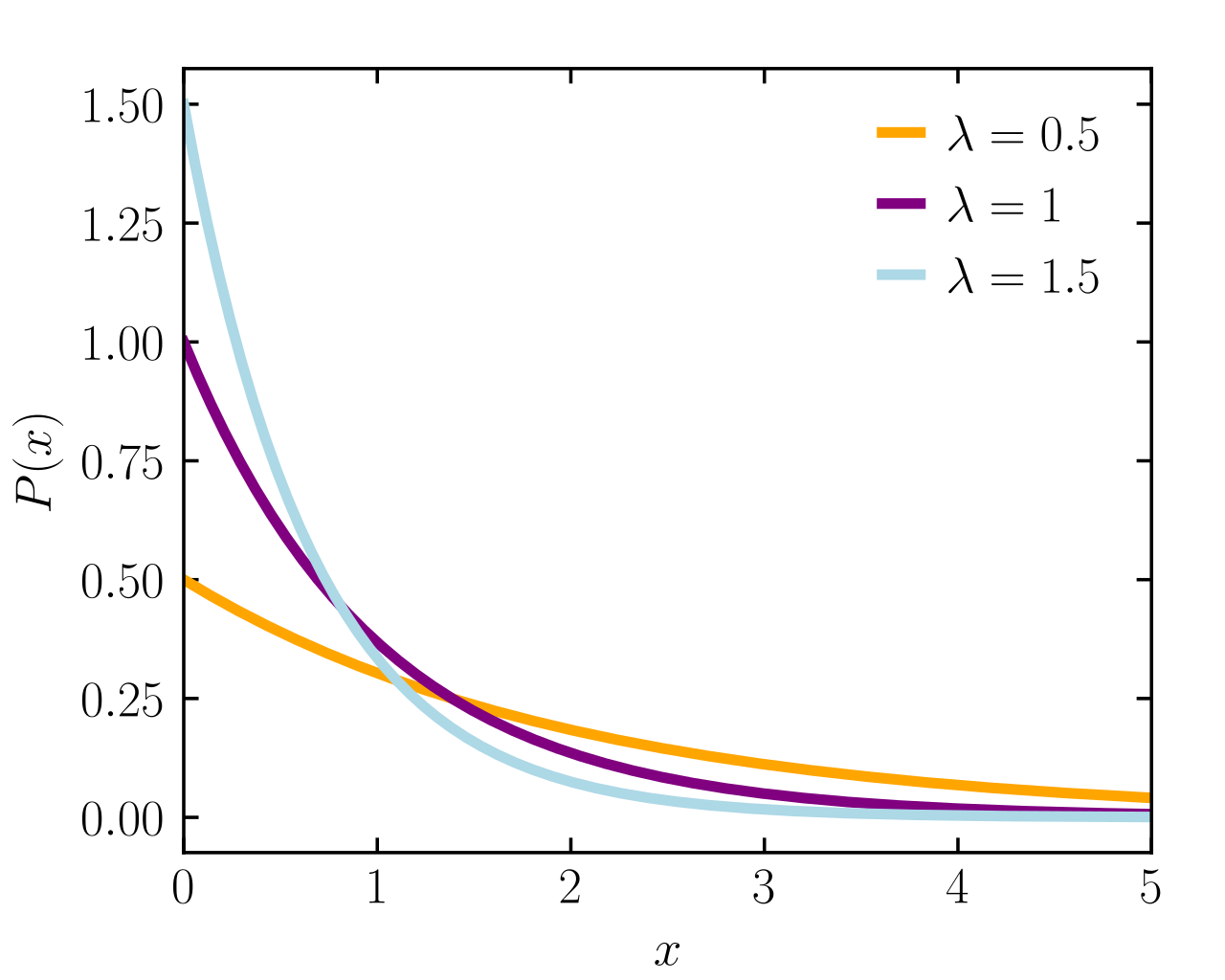
지수분포도 물론 연속형 확률분포에서 다루게 될 분포들 중 하나이다.
2. 누적분포함수($cdf$)
이제 이 확률 변수 $X$의 분포를 묘사하는 방법들 중 하나인 누적분포함수(cumulative distribution function : $cdf$)에 대해서 알아보자. 참고로 확률 변수 $X$의 분포를 묘사하는 방법들로는 $cdf$ 이외에 대표적으로 확률밀도함수(probability density function : $pdf$)<footnote> 이산형의 경우 특히 probability mass function : $pmf$ 라고 표현하기도 함</footnote>, 적률생성함수(moment-generating function : $mgf$) 등이 있다. 누적분포함수는 기호로 아래와 같이 나타낸다.
$F(x) = P(X\leq x)$
주의해야 할 점으로는 $X$의 분포 함수는 항상 연속형 또는 이산형인 것만 존재하는 것이 아닌, 혼합형도 존재할 수 있다는 점이다.
$pdf$ 와의 관계
$F(x)= \left\{\begin{matrix} \sum_{t\leq x}f(t),\, \textrm{X : discrete} \rightarrow f(x) = F(x) - F(x-1)
\\ \int_{-\infty }^{x}f(t),\, \textrm{X : continuous} \rightarrow f(x) = \frac{d}{dx}F(x)
\end{matrix}\right.$
3. 확률 변수의 기댓값
기댓값(Expectation)이란 확률변수가 가지는 분포의 중심 위치(또는 무게중심)를 나타내는 값이라고 할 수 있다. 확률변수 $X$가 $pdf$로 $f(x)$를 가질 때, $X$의 함수인 $u(X)$의 기댓값은 $E[u(X)]$로 표기하고 다음과 같이 정의된다.
$E[u(x)]= \left\{\begin{matrix} \sum_{x}u(x)f(x),\, \textrm{X : discrete}
\\ \int_{-\infty }^{\infty}u(x)f(x),\, \textrm{X : continuous}
\end{matrix}\right.$
위 기댓값의 정의를 기반으로 통계학에서 중요하게 취급되는 몇 가지 $u(X)$의 형태가 있다.
$u(X) = X$ 일 때
확률변수 $X$의 기댓값 또는 평균(Mean)이라고 하며, 분포의 중심 위치(또는 무게중심)를 나타내는 값이라고 할 수 있다.
$u(X) = (X-\mu)^2$ 일 때
확률변수 $X$의 분산이라고 한다. 또한 이것에 루트($\sqrt{\,\,\,\,\,\, }$)를 씌운 형태를 $X$의 표준편차(standard deviation)라고 하며, 분포가 평균($\mu$)로부터 퍼진 정도를 나타내는 값이다.
$u(X) = e^{tX}$ 일 때
$ M_x(t) = E(e^{tx}) = \left\{\begin{matrix} \sum e^{tx}f(x),\textrm{X : discrete}
\\ \int e^{tx}f(x)dx, \textrm{X : continuous}
\end{matrix}\right. $
이를 $X$의 적률생성함수($mgf$)라고 한다. 모든 분포에 대해서 $mgf$가 반드시 존재하는 것은 아니지만, 존재하기만 하면 유일하게(unique) 대응되는 성질을 가진다. uniqueness는 통계학에서 매우 중요한 성질이다. 참고로 $E(X^k)$ 를 $X$의 k차 적률이라고 하며, $E(X-\mu)^k$를 k차 중심적률이라 한다. 즉, 2차 중심적률은 분산과 동일하다.
4. 왜도와 첨도
(1) 왜도(Skewness)
표준화된 확률변수 $X$의 3차 적률에 해당하는 값이다. 참고로 표준화(standardized)란 확률변수에 평균($\mu$)을 빼고 표준편차($\sigma$)를 빼준 $\frac {X-\mu}{\sigma}$와 같은 작업을 하는 것을 의미한다. 예를 들어 실제 데이터 분석 시에 적합시키고자 하는 모형이 데이터셋의 각 변수들의 단위에 민감한 경우에 표준화 작업은 필수적이라고 할 수 있다. 어쨌든, 즉 왜도는 아래와 같이 정의된다.
$\frac{E(X-\mu)^3}{\sigma^3}$
왜도 값이 0이면 확률 변수의 분포는 정확하게 대칭이며, 음수이면 분포가 오른쪽으로 치우쳐져 있으며 "skewed to the left" 또는 왼쪽으로 꼬리가 긴 분포라고 정의한다. 양수이면 분포가 왼쪽으로 치우쳐져 있으며 "skewed to the right" 또는 오른쪽으로 꼬리가 긴 분포라고 정의한다.
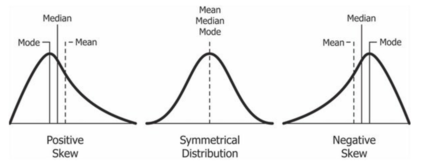
위 그림을 보면, 왜도 값이 양수인 오른쪽으로 꼬리가 긴 분포의 경우 중앙값(median)이 평균(mean) 보다 작은 값을 가지고 있다. 그 이유에 대해 조금만 직관적으로 생각해보면 따로 기억하려고 노력할 필요가 없어진다. 중앙값이란 자료를 크기순으로 배열하고 그 중간에 위치하는 값으로 자료 값의 평균적 크기에서 크게 벗어나는 이상치(outlier)에 민감하지 않다. 그에 반해 평균은 이상치에 민감한 측도로, 큰 이상치 값들이 분포하고 있는 오른쪽으로 꼬리가 긴 분포의 경우 당연히 중앙값보다 큰 값을 가지게 된다.
(2) 첨도(Kurtosis)
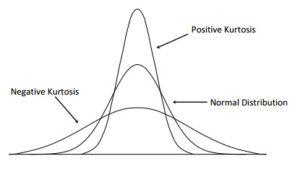
표준화된 확률변수 $X$의 4차 적률로 정의한다. 즉 아래와 같이 정의되며, 쉽게 말하면 확률변수 $X$가 가지는 분포의 뾰족한 정도를 나타내는 척도이다. 즉 분포의 산포 정도를 나타내는 값으로도 생각될 수 있다.
$\frac{E(X-\mu)^4}{\sigma^4}$ - 3
수식에서 굳이 3을 빼주는 이유는, 정규분포(Normal distribution 또는 Gaussian distribution이라고 표현하기도 함)를 갖는 확률변수의 $\frac{E(X-\mu)^4}{\sigma^4}$ 값이 3을 가지기 때문에, 이 정규분포의 첨도를 0으로 맞춰주기 위함이라고 생각된다. 또한 정규분포는 완벽히 좌우대칭을 이루는 분포로 왜도 값도 0이다.
📝 참고 문헌
나종화 (2012). 수리통계학. 자유아카데미
❗ 출처
그림 1: en.wikipedia.org/wiki/Exponential_distribution
그림 2$\cdot$3: beaconhillprivatewealth.com/viewpoints/are-you-compensated-for-your-risk
'수리통계학' 카테고리의 다른 글
| 검정력과 검정력 함수에 대해 (0) | 2020.03.30 |
|---|---|
| 기댓값과 표본평균 (0) | 2020.02.25 |
| 이산형 확률분포 (0) | 2020.02.17 |



댓글