Ensemble methods

❗️블로그 옮김:  https://www.taemobang.com

방태모

 

오늘 소개할 주제는 앙상블 기법(ensemble methods)^[각주:1]입니다. 앙상블 기법은 지도학습(supervised learning)의 대표적 기법중 하나로 여러 모형을 기반으로 예측을 결합하여 최종 결과를 내는 모형이라 할 수 있습니다. 이번 글에서는 Stacking을 제외한 가장 인기있는 대표적 앙상블 기법인 배깅(bagging)과 부스팅(boosting)을 기반으로 한 알고리즘들을 소개해보려고 해요. 수식은 최대한 배제하고 간략한 아이디어를 제공하기 위해 노력해보겠습니다.😃 다음은 배깅과 부스팅에 대한 간략한 개념 설명입니다:

 

• 배깅: 원자료로 부터 붓스트랩 샘플링을 수행하여, 각 붓스트랩 샘플을 훈련 자료(training data)로 하여 각 모형을 병렬적으로(parallel) 훈련
• 부스팅: 먼저 원자료에 대해 모형을 훈련시킨 뒤, 다음 모형은 이전 모형에 의해 발생한 오차(errors)^[각주:2]로부터 각 모형을 순차적으로(sequential) 훈련

그림 0. 의사결정나무를 이용한 배깅과 부스팅^[각주:3]

 

그림 0은 의사결정나무를 이용한 배깅과 부스팅 기법을 나타낸 것입니다. 배깅의 경우 원자료의 각 붓스트랩 샘플에 깊은 의사결정나무를 적합시키며, 부스팅의 경우 깊이가 얕은 의사결정나무를 순차적으로 적합합니다. 이 두 방법의 아이디어를 bias-variance trade-off 관점에서 풀어보겠습니다. 배깅은 각 붓스트랩 샘플에 깊은 트리를 적합시켜 과적합된 모형에 의해 분산(variance)이 커지는 문제를 모든 트리의 결과를 종합^[각주:4]하여 분산을 낮추는 아이디어를 갖습니다. 반면, 부스팅은 얕은 트리^[각주:5]를 순차적으로 적합시켜 얕은 트리에 의해 편향(bias)이 커지는 문제를 모든 트리의 결과를 종합하여 편향을 낮추는 아이디어를 갖죠. 실제 값에 가깝게 추정하기 힘든 얕은 트리와 같은 모형을 weak learner라고 하며, 그래서 우리는 부스팅 기법을 weak learners를 결합하여 strong learner를 만드는 기법이라고 표현하기도 합니다.

 

배깅과 부스팅 기법에 가장 많이 쓰이는 예측 모형은 의사결정나무(decision tree)이므로 이를 기반으로 글을 쓰려고 합니다. 앞으로 소개할 모형들은 배깅과 부스팅에 기본적인 아이디어가 깔려있으며, 모두 의사결정나무에 기반한 모형입니다. 유명한 배깅, 부스팅 기반의 알고리즘들이 모두 의사결정나무에 기반하는 이유는 의사결정나무에 배깅, 부스팅 기법을 적용하면 상당한 성능 향상을 이룰 수 있기 때문입니다. 아울러, 의사결정나무가 본질적으로 갖는 문제는 사전 또는 사후 가지치기를 한다고 해도 자료에 과적합되는 경향이 있다는 점입니다. 이러한 문제점을 해결하기 위해 배깅과 부스팅 기법에 의사결정나무를 이용하였고, 그 효과가 매우 뛰어나 배깅과 부스팅 기법에 많이 쓰여져 왔다고 생각합니다. 이제 본격적인 모형 소개를 시작해보겠습니다.

 

랜덤포레스트(Random Forest)

의사결정나무와 배깅에 대한 개념을 알고 있는 사람에게 랜덤포레스트를 최대한 간략히 설명하자면, 의사결정나무에 배깅을 수행한 것의 발전된 형태라고 할 수 있겠습니다. 발전된 형태라고 표현한 이유는 랜덤포레스트에서 각 붓스트랩 샘플에 적합되는 트리들은 가지분할 시 자료의 모든 변수^[각주:6]($X$)를 고려하는 것이 아닌, 변수들에 확률표본(random sample)을 취하여 random한 subset을 고려하게 됩니다. 그리고, 이들 중 최적의 분할을 찾아 각 트리를 적합합니다. 이를 통해 우리는 기존의 조금 더 단순한 형태인 의사결정나무에 배깅을 수행했을 때 발생하던 문제인 트리 상관(tree correlation) 문제를 해결할 수 있었습니다. 트리 상관 문제란, 말그대로 각 붓스트랩 샘플에서 적합된 트리들이 서로 상관되는 것을 말합니다. 이러한 문제가 발생하는 이유는 간단합니다. 배깅은 본래 앞서 말씀드렸다시피 깊은 트리를 적합한다고 했습니다. 그에 따라 붓스트랩을 수행하여 각각 트리를 적합한다고 해도 모든 변수를 가지고 최적의 분할을 찾다보니, 결국 각 트리에서 고려하게 되는 최적의 분할에는 큰 차이가 없는 것이죠. 즉, 비슷한 결과를 내는 여러 트리를 만들어 내게 되는 겁니다. 그래서, 결과를 종합해봤자 크게 분산을 떨어뜨리는 효과를 보지 못하는 것이죠. 이제 그림으로 랜덤포레스트의 형성 과정을 알아봅시다. 다음은 랜덤포레스트의 형성 과정을 그림으로 나타낸 것 입니다:

 

그림 1. 랜덤포레스트의 형성 과정

위 그림은 분류(classification) 문제에 대해 설명한 그림에 해당하며, 랜덤포레스트는 분류와 회귀 모두 해결할 수 있는 모형에 해당합니다. 또한 그림 2의 Step 1에서 말하는 Subset 1~Subset n을 원 자료의 붓스트랩 샘플이라고 생각하시면 됩니다.

 

AdaBoost(Adaptive Boosting)

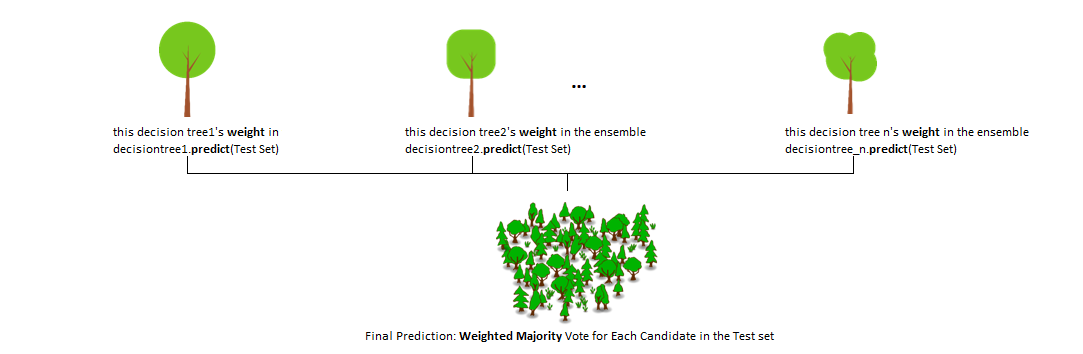
AdaBoost는 첫 번째로 소개할 부스팅 기반의 모형이며 특히 의사결정나무와 잘 작동합니다. 또한 이진 분류(binary classification)^[각주:7]에서 뛰어난 성능을 보입니다. 부스팅 모형의 주 아이디어는 상술했듯이 이전 모형의 오차로 부터 학습한다는 점입니다. AdaBoost는 오분류된 관측치^[각주:8](observations)의 가중치(weight)를 증가시키는 방법으로 학습을 진행해 나갑니다. AdaBoost의 학습 과정은 다음 그림과 설명을 참고해주시기 바랍니다.

 

그림 2.1. AdaBoost의 학습 과정-1

• Step 0: 모든 관측치들의 가중치 초기화함. 즉, $w_1 = \frac{1}{n} $ 이며, 여기서 $n$은 해당 데이터 셋의 관측치 개수를 나타냄
• Step 1: 해당 자료에 대해 트리 학습
• Step 2, 3: 학습 시킨 트리의 가중 오차율(weighted error rates, $\varepsilon$) 계산. 즉, 여기서 $\varepsilon$은 해당 트리가 얼마나 많은 예측을 잘못 수행했는지를 나타냄

해당 트리의 가중 오차율 = $\ln\frac{1-\varepsilon}{\varepsilon}$

 

즉, 각 트리의 가중치는 로짓 변환의 형태^[각주:9]로 계산된다. 좋은 성능을 보이는 트리일수록 가중이 커지고, 최종 결정에 미치는 영향이 클 것입니다. AdaBoost에는 트리가 갖는 가중치뿐만이 아닌, 각 관측치가 갖는 가중치가 존재합니다:

 

• Step 4: 오분류된 관측치의 가중치를 갱신

 

각 관측치의 가중치 $ = $ $\left\{\begin{matrix} \textrm{If it corrects, maintain the weight.} 
\\ \textrm{If it's wrong,} \: w^{new} = w^{old}*exp(\textrm{weight of this tree}) 

\end{matrix}\right.$

 

트리의 가중이 클수록, 즉 분류에 훌륭한 성능을 보이는 트리일수록 이때 오분류된 관측치는 더 큰 중요성을 갖게될 것입니다("get more boost/importance").

 

• Step 5: 사전에 설정한 트리 개수까지 Step 1으로 돌아가 위 과정 반복
• Step 6: 위와 같은 단계로 순차적으로 학습시킨 트리들의 결과를 종합하여 최종 예측 수행

그림 2.1. AdaBoost의 학습 과정-2

 

Gradient Boosting

Gradient Boosting은 또 다른 부스팅 모형입니다. Gradient Boosting은 AdaBoost처럼 각 관측치들의 가중을 갱신하는 것이 아닌, 잔차(residuals = $y_{i} - \hat{y_{i}}$)를 통하여 좀 더 직접적인 이전 모형의 오차로부터 학습을 진행합니다. 즉 Gradient Boosting에서 최소화하고자하는 목적함수(objective function)는 실제값^[각주:10]과 예측값의 차이인 잔차에 해당하죠. 이를 최소화 시키는데에 1차 기울기 계수와 2차 기울기 계수가 필요한데, 이때 경사하강법(gradient descent algorithm)을 사용하기때문에 Gradient Boosting이란 이름을 붙은 것으로 생각됩니다. 다음은 Gradient Boosting의 학습 과정을 그림으로 나타낸 것입니다:

 

그림 3. Gradient Boosting 학습 과정

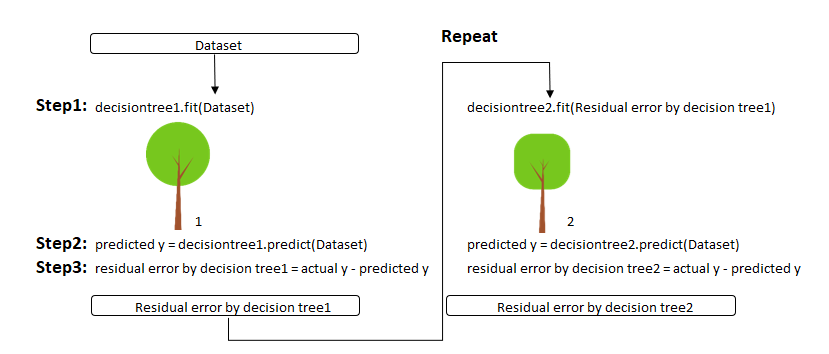
• Step 1: 원자료에 대해 의사결정나무 학습
• Step 2: 학습시킨 의사결정나무를 이용해 예측 수행
• Step 3: 예측을 수행하고 남은 잔차 계산
• Step 4: 사전에 설정한 트리 개수만큼 Step 1으로 돌아가 위 과정 반복
• Step 5: 위와 같은 단계로 순차적으로 학습시킨 트리들의 결과를 종합하여 최종 예측 수행

 

XGBoost(eXtreme Gradient Boosting)

XGBoost도 마찬가지로 의사결정나무를 기반으로 하는 또다른 부스팅 모델입니다. 모형 이름에서 드러나듯 Gradient Boosting을 좀 더 빠르고 정확하게 개선한 모델이며, Gradient Boosting과 동일한 프레임 워크를 사용합니다. 과거 XGBoost는 수 많은 Kaggle competition에서 winner solutions으로 이름을 올렸으며, 그만큼 수많은 장점을 가지고 있다고 할 수 있습니다. 논문에서 너무 강조하는 장점이 많아서 자세한 사항이 궁금하신 분들은 Chen et al. (2016)을 참고하길 바랍니다.😅 컴퓨터 과학(computer science)에 대한 지식이 없다면 논문의 중후반부는 읽기 어려울 수도 있습니다. 물론 저도 힘들었습니다.

 

여기서는 컴퓨터 과학쪽 지식을 동원해 설명할 수 있는 XGBoost의 개선점은 제외한 목적함수 부분에서의 중요한 개선점에 대해 말씀드리려고 합니다. XGBoost의 전반적인 학습과정은 Gradient Boosting에서 설명했던 것과 동일합니다. 다만, XGBoost의 목적함수는 Gradient Boosting에서 최소화하고자 했던 목적함수에 generalization errors를 줄이기 위한 목적으로 각 리프노드의 가중치를 원소로 갖는 벡터 $l_2\textrm{-norm}$을 벌점 항(penalty term)^[각주:11]을 한번 더 높이는 것이죠. 그리고, Gradient Boosting의 목적함수에 벌점 항을 도입한 것이므로, 벌점 항을 조절하는 모수를 0으로 둔다면 기존의 Gradient Boosting 모형과 동일한 목적함수를 갖게 됩니다.

 

Light GBM(Light Gradient Boosting Model)

Light GBM의 모티베이션은 XGBoost의 긴 학습 시간이라 할 수 있습니다. XGBoost보다 학습 시간이 짧음에도 Light GBM은 그와 비슷한 성능을 내거나 조금 더 나은 성능을 보이는 경우도 때때로 있습니다. Light GBM의 트리성장은 앞서 다루었던 트리기반 알고리즘들과는 조금 다르게 진행됩니다. 앞서 다루었던 트리기반 알고리즘들은 트리를 성장시킬 때 level-wise(또는 depth-wise) 알고리즘을 이용하는 반면, Light GBM은 leaf-wise 알고리즘을 이용합니다:

 

그림 5. Level-wise 알고리즘^[각주:12]

 

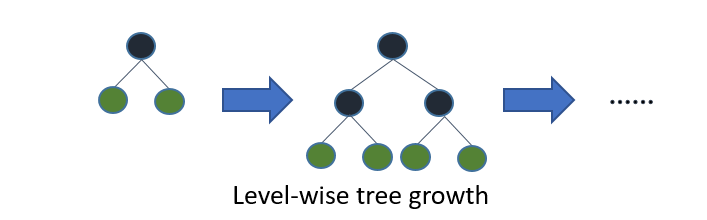
여기서 level은 트리의 깊이, leaf는 트리의 리프노드로 맨 아래 수준에 해당하는 노드를 의미합니다. Level-wise란 그림 5와 같이 트리를 성장시키는 것을 말하며, 이것이 일반적인 트리 기반 알고리즘들이 사용하는 방법이라 할 수 있습니다.

 

 

그림 6. Leaf-wise 알고리즘

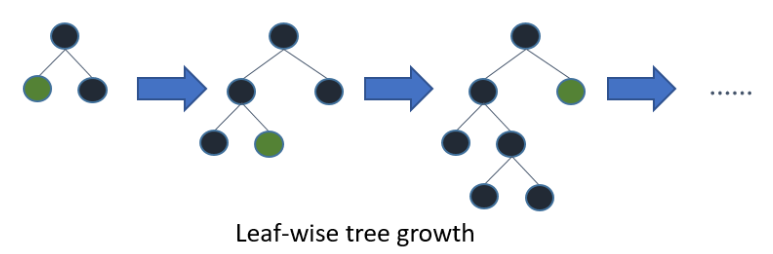
Light GBM은 트리를 성장시킬 때에 그림 6과 같은 leaf-wise 알고리즘을 사용합니다다. 그림 5와 그림 6을 보면 알 수 있겠지만, leaf-wise 방법을 사용하여 트리를 성장시키는 것이 트리를 우리가 원하는 방향으로 좀 더 세밀하게 성장시킬 수 있을거라는 생각이 듭니다. 즉, 더 세부적으로 트리를 성장시킬 수 있어 목적함수의 값을 좀 더 작게 감소시킬 수 있으며, 결과적으로 앞서 다루었던 트리기반 부스팅 모형에서는 얻기힘든 훨씬 더 좋은 성능을 얻을 수 있게 되는 것이죠. 사실 leaf-wise 알고리즘을 택할 경우 결국 모형의 복잡도(complexity)의 증가를 초래하기 때문에 오히려 과적합을 야기할 수 있다고 생각할 수 있으나, 자료의 크기가 충분히 크고(1만개 이상의 관측치) 분할이 일어날 수 있는 트리의 최대 깊이를 조정하여 충분히 극복할 수 있다고 합니다. 다만, 자료의 수가 작을 경우 leaf-wise 알고리즘은 과적합 우려가 매우 크다고 합니다. 즉, Light GBM은 대용량 데이터에 적합한 트리기반 부스팅 방법이라 할 수 있겠죠.

 

그래서 이렇게 leaf-wise 알고리즘을 이용해 트리를 좀더 세부적으로 성장시키는 Light GBM이 어떻게 XGBoost보다도 더 빠른 속도를 낼 수 있을까요? 짧은 구글링을 통해 얻은 이유는, Light GBM은 Approximates the split이라는 분할 알고리즘을 사용하기 때문이라는 것입니다. 사실 이 부분은 XGBoost의 논문 Chen et al. (2016)에서도 모델 형성의 속도를 높이기 위해 사용한 알고리즘으로 제시되어있어서, 구글링을 통해 얻은 이유가 정확한지는 잘 모르겠습니다. 사실 Light GBM의 논문을 들여다보진 않았습니다..😂

 

맺음말

본 글에서는 tabluar data에 관한 예측 모델링에서 흔히 접할 수 있는 앙상블 기법들, 그 중에서도 크게는 배깅, 부스팅에 기반한 알고리즘들에 대해 알아보았습니다. 최대한 수식은 지양한채로 각 알고리즘의 모티베이션, 차이점에 대해 이해할 수 있도록 적어보았습니다. 좀 더 깊은 수학적 백그라운드가 궁금하신 분들^[각주:13]에게 이 글이 충분한 만족감을 드리긴 어려울 것 같습니다. 본 글에서 소개한 알고리즘들은 tabluar data에 관한 예측 모델링에 상당히 좋은 성능을 갖습니다. 실제로, NVIDIA AI에서 근무하고 있는 기계학습 전문가, 캐글 그랜드마스터가 이런 말을 하기도 했습니다:

I keep saying XGBoost is better than NNs in many tabular data and time series forecasting, but if I have only half a day then I'll run a deep learning model. Indeed, feature engineering for XGBoost requires data intimacy which takes some time.

— JFPuget 💉💉💉🇺🇦 (@JFPuget) March 31, 2022

Feature engineering에 충분한 시간을 투자한다면 XGBoost는 tabluar data, 그리고 심지어는 시계열의 예측 모델링에서도 인공신경망(NN, Neural Net) 기반의 예측 모형보다 더 좋은 성능을 보여준다고 합니다. 다만, 시간이 얼마 없다면 Feature engineering 과정이 따로 필요없는 인공신경망 기반 예측모형을 이용한다고 하네요. 흥미로운 의견이네요. 실무에서 예측 모델링을 수행하실 때, 이 의견을 참고해보셔도 좋을 것 같습니다. 그럼, 이만 줄이겠습니다.

 

웹페이지 인용

[1] Basic Ensemble Learning (Random Forest, AdaBoost, Gradient Boosting)- Step by Step Explained[Towards data science]. (2020, Feb 12).

[2] XGBoost Algorithm: Long May She Reign![Towards data science]. (2020, Feb 12).

[3] Which algorithm takes the crown: Light GBM vs XGBOOST?[Analytics Vidhya]. (2020, Feb 12).

---

1. 앙상블 모형, 앙상블 방법, 앙상블 알고리즘 등이라 표현하기도 함 [본문으로]
2. mistakes라 표현하기도 함 [본문으로]
3. 그림 0-그림 3 출처. Basic Ensemble Learning (Random Forest, AdaBoost, Gradient Boosting)- Step by Step Explained[Towards data science]. (2020, Feb 12). [본문으로]
4. 일반적으로 분류의 경우 다수결(majority vote), 회귀의 경우 평균 [본문으로]
5. 특히 트리의 깊이가 1인 한번만 가지 분할이 수행되는 트리는 스텀프(stump)라 칭함 [본문으로]
6. 통계학에서는 예측변수(predictor)라 표현하며, 기계학습(machine learning)에서는 특성(feature)라고 표현함 [본문으로]
7. $y$의 레이블이 2개인 경우 [본문으로]
8. 기계학습에서는 데이터포인트(data point)라 표현하기도 함 [본문으로]
9. 오즈에 자연로그를 씌운 형태 [본문으로]
10. 관측값이라고도 표현 [본문으로]
11. 벌점 회귀(penalized regression) 기법 중 하나인 Ridge regression의 벌점항 형태와 같음[/foonote]을 도입하여 regularized된 목적함수를 최소화 시킨다고 할 수 있습니다. 즉, 벌점을 통해 일반화 성능[footnote]unobserved data에 관한 성능 [본문으로]
12. 그림 5-그림 6 출처. Which algorithm takes the crown: Light GBM vs XGBOOST?[Analytics Vidhya]. (2020, Feb 12). [본문으로]
13. 각 알고리즘의 논문이나 ESL II를 참고해 보시는 것을 추천드립니다. [본문으로]